30, 60 և 45 աստիճանի անկյունների սինուսը, կոսինուսը և տանգենսը

\(30°\) անկյան եռանկյունաչափական ֆունկցիաներ արժեքները

Դիտարկենք \(C\) ուղիղ անկյունով \(ABC\) ուղղանկյուն եռանկյունը և ենթադրենք, որ

α = 30^{°}

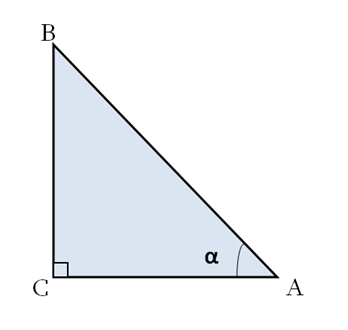
Ուշադրություն

Հիշենք, որ ուղղանկյուն եռանկյան

30^{°}

-ի անկյան դիմացի էջը հավասար է ներքնաձիգի կեսին:

\sin 30^{°} = \frac{BC}{AB} = \frac{BC}{2 BC} = \frac{1}{2}

{\sin^{2} 30}^{°} + {\cos^{2} 30}^{°} = 1

եռանկյունաչափական հիմնական առնչության հիման վրա՝

\cos 30^{°} = \sqrt{1 - \sin^{2} 30^{°}} = \sqrt{1 - \frac{1}{4}} = \frac{\sqrt{3}}{2}

Ունենք

30^{°}

-ի անկյան սինուսն ու կոսինուսը: Գտնում ենք նրանց հարաբերությունը՝ տանգենսը.

tg 30^{°} = \frac{\sin 30^{°}}{\cos 30^{°}} = \frac{1}{2} : \frac{\sqrt{3}}{2} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}

Ուշադրություն

Այսպիսով՝

\sin 30^{°} = \frac{1}{2}

\cos 30^{°} = \frac{\sqrt{3}}{2}

tg 30^{°} = \frac{\sqrt{3}}{3}

\(60°\) անկյան եռանկյունաչափական ֆունկցիաներ արժեքները

Եթե ուղղանկյուն եռանկյան սուր անկյուններից մեկը

60^{°}

է, ապա մյուս սուր անկյունը

30^{°}

է, և մենք գալիս ենք դիտարկած դեպքին:

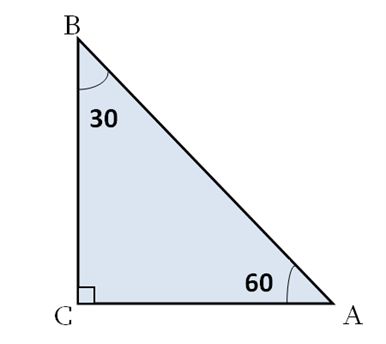
Քանի որ անկյունները տեղերով փոխվեցին, ապա տեղերով փոխվեցին նաև նրանց դիմացի և կից էջերը, ուրեմն նաև սինուսն ու կոսինուսը: Ուրեմն՝

\cos 60^{°} = \frac{1}{2}

\sin 60^{°} = \frac{\sqrt{3}}{2}

Որտեղից՝

tg 60^{°} = \frac{\sin 60^{°}}{\cos 60^{°}} = \frac{\sqrt{3}}{2} : \frac{1}{2} = \sqrt{3}

Ուշադրություն

Այսպիսով`

\sin 60^{°} = \frac{\sqrt{3}}{2}

\cos 60^{°} = \frac{1}{2}

tg 60^{°} = \sqrt{3}

\(45°\) անկյան եռանկյունաչափական ֆունկցիաներ արժեքները

Եթե

{α = 45}^{°}

, ապա մյուս սուր անկյունը ևս

45^{°}

է, և մենք ստանում ենք հավասարասրուն ուղղանկյուն եռանկյուն:

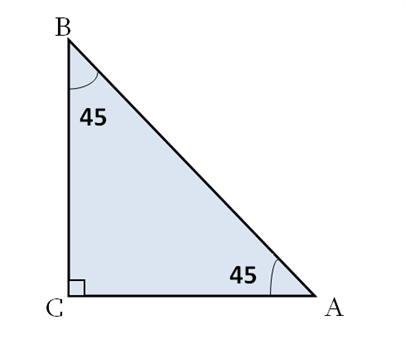
Հավասարասրուն ուղղանկյուն եռանկյան էջերը հավասար են, ուրեմն հավասար են նաև

45^{°}

-ի անկյան սինուսն ու կոսինուսը: Հետևաբար, տանգենսը, որպես դրանց հարաբերություն, հավասար է մեկի՝

tg 45^{°} = \frac{\sin 45^{°}}{\cos 45^{°}} = 1

{\sin^{2} 45}^{°} + {\cos^{2} 45}^{°} = 1

հիմնական առնչության հիման վրա՝

\begin{array}{l} \sin^{2} 45^{°} + \cos^{2} 45^{°} = 2 \sin^{2} 45^{°} = 1 \\ \sin^{2} 45^{°} = \frac{1}{2} \\ \sin 45^{°} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \end{array}

Ուշադրություն

Այսպիսով՝

\sin 45^{°} = \frac{\sqrt{2}}{2}

\cos 45^{°} = \frac{\sqrt{2}}{2}

tg 45^{°} = 1

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Սխա՞լ ես գտել

2. 30, 60 և 45 աստիճանի անկյունների սինուսը, կոսինուսը և տանգենսը