Եռանկյունաչափական ֆունկցիաների արժեքների աղյուսակ — դաս։ Երկրաչափություն, 8-րդ դասարան.

Եռանկունաչափական ֆունկցիաների արժեքները, որոնք պետք է անգիր իմանալ

Մենք արդեն գիտենք \(30\)

°

, \(45\)

°

և \(60\)

°

-ի անկյունների սինուսը, կոսինուսը և տանգենսը: Տեղադրենք դրանք հետևյալ աղյուսակի մեջ:

	\(30\) $°$	\(45\) $°$	\(60\) $°$
\(sin\) $α$ \(\)	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$
\(cos\) $α$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$
\(tg\) $α$ \(\)	$\frac{\sqrt{3}}{3}$	\(1\ \)	$\sqrt{3}$

Դու պիտի փորձես անգիր անել այս աղյուսակը:

Մնացած անկյունների համար եռանկյունաչափական ֆունկցիաների արժեքները մենք կուսումնասիրենք հետագայում: Դու կարող ես դրանք գտնել հատուկ աղյուսակներում կամ հաշվել հաշվիչի միջոցով:

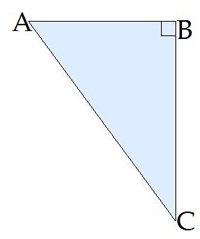
Օրինակ

Տրված է՝ \(AB =\)\(6\)\(սմ\),

∡ A = 60 °

Հաշվել \(AC\) -ն:

Պահանջվող հատվածը ուղղանկյուն եռանկյան ներքնաձիգն է, իսկ տրվածը՝ կից էջն է: Ուրեմն, պետք է օգտագործել կոսինուսը:

\begin{array}{l} cosA = \frac{AB}{AC} \\ AC = \frac{AB}{\cos A} = 6 : \frac{1}{2} = 12 սմ \end{array}

Ուղղանկյուն եռանկյան հատկությունների կիրառումը

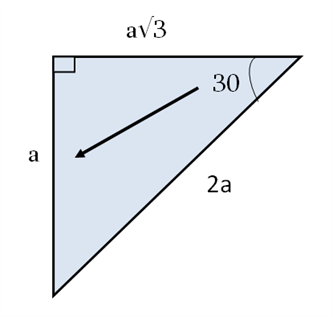
Ուղղանկյուն եռանկյան \(30\)

°

-ի դիմացի էջը հավասար է ներքնաձիգի կեսին:

Ուղղանկյուն եռանկյան \(60\)

°

-ի դիմացի էջը հավասար է փոքր էջի և

\sqrt{3}

-ի արտադրյալին:

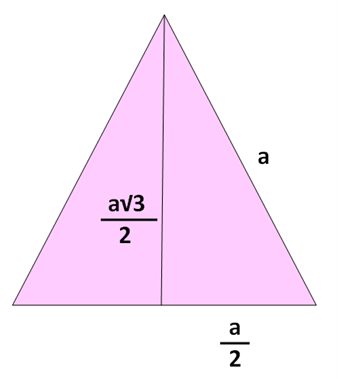
Այս արժեքները հարմար է օգտագործել հավասարակողմ եռանկյան բարձրությունը որոշելիս:

Հավասարակողմ եռանկյան անկյունը \(60\)

°

է, իսկ ներքնաձիգը կիսում է այդ անկյունը:

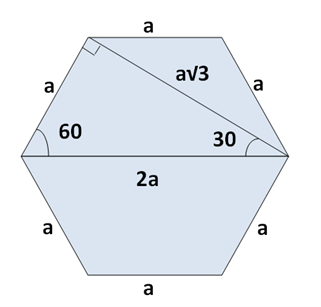
Կանոնավոր վեցանկյան մեջ մեծ անկյունագիծը, փոքր անկյունագիծը և կողմը կազմում են ուղղանկյուն եռանկյուն, որի անկյուններից մեկը \(30\)

°

է:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ