Եռանկյունաչափական հիմնական առնչությունը — դաս։ Երկրաչափություն, 8-րդ դասարան.

Սուր անկյան եռանկյունաչափական ֆունկցիաները

Դիտարկենք \(C\) ուղիղ անկյունով \(ABC\) ուղղանկյուն եռանկյունը:

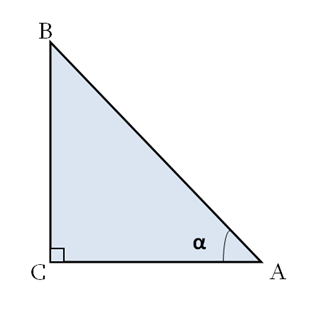
1) Ուղղանկյուն եռանկյան սուր անկյան սինուս կոչվում է այդ անկյան դիմացի էջի հարաբերությունը ներքնաձիգին:

2) Ուղղանկյուն եռանկյան սուր անկյան կոսինուս կոչվում է այդ անկյան կից էջի հարաբերությունը ներքնաձիգին:

3) Ուղղանկյուն եռանկյան սուր անկյան տանգենս կոչվում է այդ անկյան դիմացի էջի հարաբերությունը կից էջին:

\begin{array}{l} \sin α = \frac{BC}{AB}, \cos α = \frac{AC}{AB}, \\ tg α = \frac{BC}{AC} \end{array}

Այս բանաձևերից ստանում ենք՝

\frac{\sin α}{\cos α} = \frac{BC}{AB} : \frac{AC}{AB} = \frac{BC}{AB} \cdot \frac{AB}{AC} = \frac{BC}{AC} = tg α

Ուղղանկյուն եռանկյան սուր անկյան տանգենսը հավասար է այդ անկյան սինուսի և կոսինուսի հարաբերությանը՝

tg α = \frac{\sin α}{\cos α}

Եռանկյունաչափական հիմնական առնչությունը

Ուղղանկյուն եռանկյան

α

սուր անկյան սինուսի և կոսինուսի քառակուսիների գումարը հավասար է \(1\) -ի`

{\sin α}^{2} + {\cos α}^{2} = 1

Այս հավասարությունը տեղի ունի ցանկացած

α

անկյան համար և կոչվում է եռանկյունաչափական հիմնական առնչություն:

Մենք արդեն հանդիպել ենք Պյութագորասի թեորեմի բազմաթիվ կիրառությունների: Այս կարևոր նույնությունը ևս ապացուցվում է Պյութագորասի թեորեմի օգնությամբ:

{\sin α}^{2} + {\cos α}^{2} = \frac{{BC}^{2}}{{AB}^{2}} + \frac{{AC}^{2}}{{AB}^{2}} = \frac{{BC}^{2} + {AC}^{2}}{{AB}^{2}}

Վերջին հավասարության համարիչում գրված է \(ABC\)\ ուղղանկյուն եռանկյան էջերի քառակուսիների գումարը, իսկ հայտարարում՝ ներքնաձիգի քառակուսին:

Ըստ Պյութագորասի թեորեմի, դրանք իրար հավասար են՝

{BC}^{2} + {AC}^{2} = {AB}^{2}

Այսպիսով, ստացանք՝

{\sin α}^{2} + {\cos α}^{2} = 1

հիմնական առնչությունը:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Սխա՞լ ես գտել

1. Եռանկյունաչափական հիմնական առնչությունը