
















Պրիզմայի անկյունագծերն ու անկյունագծային հատույթները
Պրիզմայի անկյունագիծը այն հատվածն է, որը միացնում է պրիզմայի նույն հարթության մեջ չգտնվող երկու գագաթները:
Անկյունագիծ չունի միայն եռանկյուն պրիզման:
Եթե ուղիղ պրիզմայի հիմքի անկյունագծերը հավասար են, ապա պրիզմայի անկյունագծերը ևս հավասար են:
Օրինակ, խորանարդի, կանոնավոր քառանկյուն բուրգի և ուղղանկյունանիստի անկյունագծերը հավասար են՝ \(DF = EC\), քանի որ \(DB = CA\)
Եթե զուգահեռանիստի հիմքում զուգահեռագիծ է, ապա , քանի որ
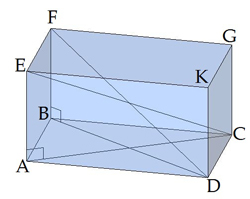
Նշեցինք, որ եռանկյուն պրիզման անկյունագիծ չունի:
Քառանկյուն պրիզման ունի 4 անկյունագիծ:
\(n\)-անկյուն պրիզման ունի \(n·(n-3)\) անկյունագիծ:
Անկյունագծային հատույթը պրիզմայի այն հատույթն է, որն անցնում է նույն նիստում չգտնվող երկու կողմնային կողերով:
Յուրաքանչյուր անկյունագծային հատույթ պարունակում է պրիզմայի երկու անկյունագծերը:
Ուղիղ պրիզմայի անկյունագծային հատույթը ուղղանկյուն է:
Թեք պրիզմայի անկյունագծային հատույթը զուգահեռագիծ է:
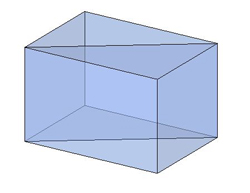
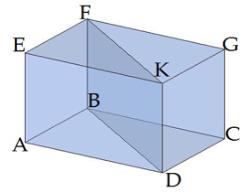
Ուշադրություն
Կանոնավոր վեցանկյունն ունի երկու տեսակի անկյունագծեր՝ կարճ և երկար:
Հետևաբար, վեցանկյուն պրիզման ևս ունի երկու տեսակի անկյունագծեր:
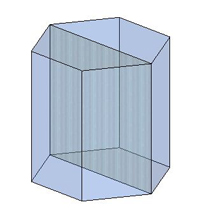
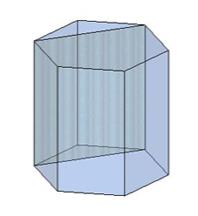
Օրինակ
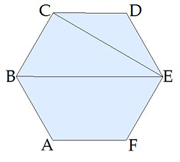
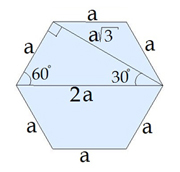
Գտնենք կանոնավոր վեցանկյան անկյունագծերը, եթե տրված է նրա կողմը:
\(CE\)-ն վեցանկյան կարճ անկյունագծերից մեկն է, \(BE\)-ն՝ երկար անկյունագծերից մեկը:
Քանի որ կանոնավոր վեցանկյան բոլոր անկյունները \(120\)° են, ապա գտնում ենք \(30\)° անկյունով ուղղանկյուն եռանկյունը և օգտագործում ենք նրա կողմերի առնչությունները:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009