
















Եթե բուրգի կողմնային նիստերը հիմքի հարթության հետ կազմուն են հավասար երկնիստ անկյուններ, ապա բոլոր այդ նիստերի բարձրությունները հավասար են, իսկ հիմքի հարթության վրա բուրգի գագաթի պրոյեկցիան հիմքի բազմանկյան ներգծյալ շրջանագծի կենտրոնն է:
Վերևից նայելիս այդպիսի բուրգն ունի հետևյալ տեսքը:
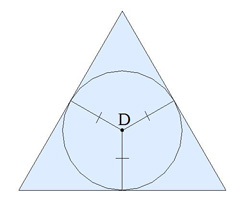
Բուրգը կարող է ունենալ հիմքին առընթեր հավասար երկնիստ անկյուններ, եթե նրա հիմքի բազմանկյանը հնարավոր է ներգծել շրջանագիծ:
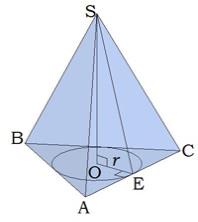
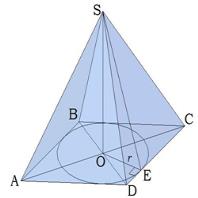
Հիշենք կապերը բազմանկյուններում, որոնց շուրջ հնարավոր է արտագծել շրջանագիծ:
| Բազմանկյունը | Ներգծյալ շրջանագծի կենտրոնը | Շառավիղը |
կամայական եռանկյուն | անկյունների կիսորդների հատման կետը | , \(p\)-ն կիսապարագիծն է |
շեղանկյուն | անկյունագծերի հատման կետը | \(r\)-ը շեղանկյան բարձրության կեսն է |
Ս. Հակոբյան, Երկրոչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009: