
















Եթե բուրգի կողմնային կողերից մեկը ուղղահայաց է հիմքի հարթությանը, ապա այդ հարթության վրա բուրգի գագաթի պրոյեկցիան հիմքի գագաթներից մեկն է:
Այս նկարում բուրգի \(DA\) կողմնային կողը ուղղահայաց է հիմքի հարթությանը:
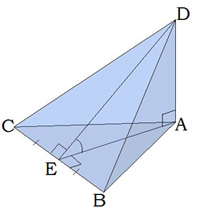
\(DA\)-ն ուղղահայաց է հիմքին, այն բուրգի բարձրությունն է:
\(DAC\) և \(DAB\) եռանկյուններն ուղղանկյուն են, \(DEA\)-ն հիմքին առընթեր երկնիստ անկյունն է:
Այս նկարում բուրգի հիմքն ուղղանկյուն է:
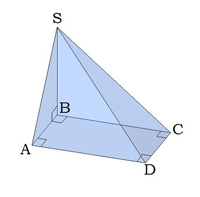
\(SB\) կողն ուղղահայաց է հիմքին, այն բուրգի բարձրությունն է:
\(SBA\) և \(SBC\) եռանկյունները ուղղանկյուն են:
Օրինակ
Քանի որ հիմքը ուղղանկյուն է, \(SAD\) և \(SCD\) եռանկյունները ևս ուղղանկյուն են:
Ապացուցենք այս պնդումը երեք ուղղահայացների թեորեմի միջոցով:
Քանի որ \(AD\)-ն ուղղահայաց է \(SA\) թեքի \(AB\) պրոյեկցիային, ապա այն ուղղահայաց է նաև \(SA\) թեքին:
Քանի որ \(CD\)-ն ուղղահայաց է \(SC\) թեքի \(BC\) պրոյեկցիային, ապա այն ուղղահայաց է նաև \(SC\) թեքին:
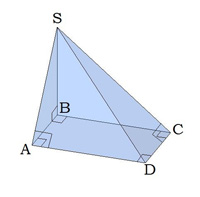
Այսպիսով,
Հետևաբար, \(SAD =\) և \(SAD\)-ն ուղղանկյուն եռանկյուն է:
Նույն ձևով ապացուցում ենք, որ \(SCD\)-ն ուղղանկյուն եռանկյուն է՝
Աղբյուրները
Ս. Հակոբյան, Երկրոչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009: