
















Եթե բուրգի կողմնային կողերը հիմքի հարթության հետ կազմում են հավասար անկյուններ, ապա կողերը հավասար են, իսկ հիմքի հարթության վրա բուրգի գագաթի պրոյեկցիան հիմքի բազմանկյան արտագծյալ շրջանագծի կենտրոնն է:
Վերևից նայելիս այդպիսի բուրգն ունի հետևյալ տեսքը:
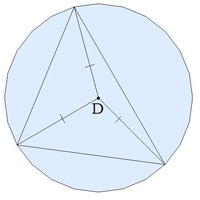
Բուրգի կողմնային կողերը կարող են հավասար լինել միայն այն դեպքում, եթե նրա հիմքին հնարավոր է արտագծել շրջանագիծ:
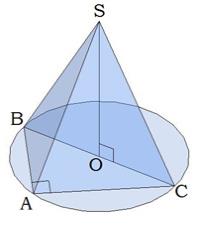 զ
զ 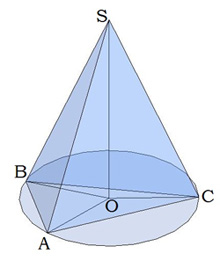
Հիշենք կապերը բազմանկյուններում, որոնց շուրջ հնարավոր է արտագծել շրջանագիծ:
| Բազմանկյունը | Արտագծյալ շրջանագծի կենտրոնը | Շառավիղը |
կամայական եռանկյուն | միջնուղղահայացների հատման կետը | \(a, b, c\) թվերը եռանկյան կողմերն են |
| հավասարասրուն եռանկյուն | միջնուղղահայացների հատման կետը գտնվում է հիմքին տարված բարձրության վրա | |
| ուղղանկյուն եռանկյուն | ներքնաձիգի միջնակետը | \(R\)-ը ներքնաձիգի կեսն է |
| ուղղանկյուն | անկյունագծերի հատման կետը | \(R\)-ը անկյունագծի կեսն է |
Աղբյուրները
Ս. Հակոբյան, Երկրոչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009: