Քառակուսային ֆունկցիայի գրաֆիկը

y = a x^{2} + bx + c

, որտեղ \(a\)-ն, \(b\)-ն, \(c\)-ն իրական թվեր են և \(a\)

\neq

\(0\) կոչվում է քառակուսային ֆունկցիա:

Քառակուսային ֆունկցիայի գրաֆիկը պարաբոլ է:

Քառակուսային ֆունկցիայի \(D(f)\) որոշման տիրույթը բոլոր իրական թվերի բազմությունն է:

Քառակուսային ֆունկցիայի \(E(f)\) արժեքների բազմությունը կախված է պարաբոլի գագաթի \(y\) կոորդինատից և պարաբոլի ճյուղերի ուղղվածությունից:

\(a\) գործակիցը որոշում է պարաբոլի ճյուղերի ուղղվածությունը:

Եթե \(a > 0\), ապա ճյուղերը ուղղված են դեպի վերև:
Եթե \(a < 0\), ապա ճյուղերը ուղղված են դեպի ներքև:

\(c\) գործակիցը ցույց է տալիս, թե որ կետում է պարաբոլը հատում \(Oy\) առանցքը:

Քառակուսային ֆունկցիայի գրաֆիկը կառուցելու համար պետք է՝

1) հաշվել պարաբոլի գագաթի կոորդինատները: Աբսցիսը գտնում ենք

x_{0} = \frac{- b}{2 a}

բանաձևով, իսկ

y_{0}

օրդինատը գտնում ենք՝ տեղադրելով

x_{0}

աբսցիսը ֆունկցիայի բանաձևի մեջ,

2) կոորդինատային հարթության վրա նշել գտնված գագաթը և տանել պարաբոլի համաչափության առանցքը,

3) որոշել պարաբոլի ճյուղերի ուղղվածությունը,

4) նշել պարաբոլի և \(Oy\) առանցքի հատման կետը,

5) ընտրելով \(x\) աբսցիսի անհրաժեշտ արժեքները, կազմել ֆունկցիայի արժեքների աղյուսակը:

Լուծելով

a x^{2} + bx + c = 0

քառակուսային հավասարումը, գտնում ենք պարաբոլի հատման կետերը \(Ox\) առանցքի հետ:

Եթե \(D > 0\)), ապա կա երկու հատման կետ:

Եթե \(D < 0\), ապա պարաբոլը չի հատում \(Ox\) առանցքը:

Եթե \(D = 0\), ապա պարաբոլի գագաթը գտնվում է \(Ox\) առանցքի վրա:

1. Կառուցենք

y = x^{2} - 2 x - 1

ֆունկցիայի գրաֆիկը:

\begin{array}{l} x_{0} = \frac{- b}{2 a} = \frac{2}{2} = 1 \\ y_{0} = 1^{2} - 2 \cdot 1 - 1 = - 2 \end{array}

Քանի որ \(a = 1 > 0\), ապա պարաբոլի ճյուղերը ուղղված են դեպի վերև:

Պարաբոլը \(Oy\) առանցքը հատում է \((0; -1)\) կետում:

\(x\)	\(2\)	\(3\)	\(4\)
\(y\)	\(-1\)	\(2\)	\(7\)

Համաչափ կառուցում ենք պարաբոլի ձախ կողմը:

2. Կառուցենք

y = - 2 x^{2} + 4 x

ֆունկցիայի գրաֆիկը:

Հաշվում ենք քառակուսային հավասարման արմատները՝

\begin{array}{l} - 2 x^{2} + 4 x = 0 \\ x (- 2 x + 4) = 0 \\ x = 0, - 2 x + 4 = 0 \\ x = 2 \\ x_{1} = 0 x_{2} = 2 \end{array}

Գտնում ենք գագաթի կոորդինատները՝

\begin{array}{l} x_{0} = \frac{- 4}{2 \cdot (- 2)} = 1 \\ y_{0} = - 2 \cdot 1^{2} + 4 \cdot 1 = 2 \end{array}

Բավական է գտնել ֆունկցիայի արժեքը \(x = 3\) կետում՝

y = - 2 \cdot {(3)}^{2} + 4 \cdot 3 = - 18 + 12 = - 6

Համաչափ գտնում ենք, որ, եթե \(x = -1\), ապա \(y = -6\):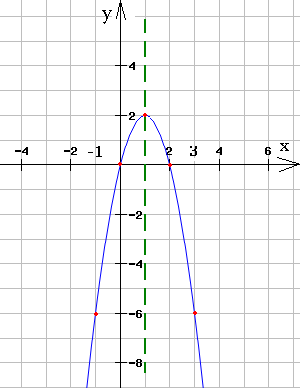

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:

Սխա՞լ ես գտել

3. Քառակուսային ֆունկցիայի գրաֆիկը