Ռացիոնալ անհավասարումների համակարգ — դաս։ Հանրահաշիվ, 9-րդ դասարան.

Փոփոխականի այն արժեքները, որոնց դեպքում համակարգի անհավասարումներից յուրաքանչյուրը վերածվում է ճիշտ անհավասարության, կոչվում են \(անհավասարությունների\) \(համակարգի\)\(լուծումներ\)\(:\)

Ռացիոնալ անհավասարումների համակարգը լուծելու համար, պետք է լուծել համակարգի յուրաքանչյուր անհավասարումը և այնուհետև գտնել ստացված լուծումների բազմությունների ընդհանուր մասը (հատումը): Դա հենց կլինի համակարգի բոլոր լուծումների բազմությունը:

Լուծել համակարգը՝ նշանակում է գտնել նրա բոլոր լուծումները:

Լուծենք հետևյալ համակարգը՝

\{\begin{cases} 2 x - 1 > 1 \\ (x + 6) (x - 4) \geq 0 \end{cases}

1. Լուծենք առաջին` գծային անհավասարումը:

\begin{array}{l} 2 x - 1 > 1 \\ 2 x > 2 \\ x > 1 \end{array}

Այս անհավասարման լուծումների բազմություննն է՝

x \in (1; + \infty)

2. Լուծենք երկրորդ՝ քառակուսային անհավասարումը՝

(x + 6) (x - 4) \geq 0

Գտնում ենք եռանդամի զրոները՝

\begin{array}{l} x + 6 = 0 x - 4 = 0 \\ x = - 6 x = 4 \end{array}

Գտնված զրոները տեղադրում ենք կոորդինատային առանցքի վրա, պարզում եռանդամի նշանները առաջացած միջակայքերում և ընտրում այն միջակայքը, որտեղ ֆունկցիայի արժեքները մեծ են կամ հավասար զրոյից:

Այս անհավասարման լուծումների բազմություննն է՝

x \in (- \infty; - 6] \cup [4; + \infty)

3. Կոորդինատային առանցքի վրա տեղադրենք երկու քայլերում ստացած բազմությունները և գտնենք դրանց հատումը:

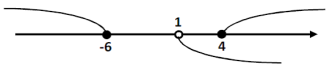
Պատասխան՝

[4; + \infty)

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Ռացիոնալ անհավասարումների համակարգ

Տեսություն