1. Բնական, ամբողջ և ռացիոնալ թվեր

Եթե բնական թվերին միացնել \(0\) թիվը և բոլոր բացասական ամբողջ թվերը՝ \(-1, -2, -3, -4,..., \), ապա ստացված բազմությունն անվանում են ամբողջ թվերի բազմություն և նշանակում են $\mathrm{\mathbb{Z}}$ տառով:
Եթե ամբողջ թվերին միացնել բոլոր սովորական կոտորակները՝ $\frac{1}{3},\frac{51}{52},-\frac{8}{5},...$, ապա ստացված բազմությունը անվանում են ռացիոնալ թվերի բազմություն և նշանակում են $\mathrm{\mathbb{Q}}$ տառով:

Ռացիոնալ թվերի $\mathrm{\mathbb{Q}}$ բազմությունը բաղկացած է $\frac{m}{n};-\frac{m}{n}$ տեսքի թվերից (որտեղ \(m\)-ը և \(n\) -ը բնական թվեր են) և \(0\) թվից:

Հասկանալի է, որ $\mathrm{\mathbb{N}}$ -ը $\mathrm{\mathbb{Z}}$ -ի ենթաբազմությունն է, իսկ $\mathrm{\mathbb{Z}}$ -ը $\mathrm{\mathbb{Q}}$ -ի ենթաբազմությունն է: Մաթեմատիկայում այս իրավիճակը նշանակում են այսպես՝ $\mathrm{\mathbb{N}}\subset \mathrm{\mathbb{Z}};\mathrm{\mathbb{Z}}\subset \mathrm{\mathbb{Q}}$:

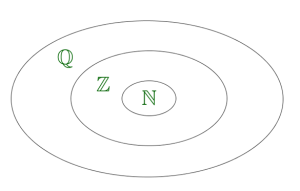
$\subset$ նշանը ցույց է տալիս, որ մի բազմություն ընկած է մյուսի մեջ:

$x\in X$ գրառումը նշանակում է, որ \(x\) -ը \(X\) բազմության տարր է:

$A\subset B$ գրառումը նշանակում է, որ \(A\) բազմությումը \(B\) բազմության մաս է: Մաթեմատիկայում ընդունված է ասել, որ \(A\) -ն \(B\) -ի ենթաբազմություն է:

Ցույց տալու համար, որ \(x\) -ը չի պատկանում \(X\) բազմությանը, կամ, որ \(A\) -ն \(B\) -ի, ենթաբազմությունը չէ, կիրառում են նույն նշանակումները, բայց թեք գծով հատած՝ $x\notin X,A\not\subset B$:

Բերենք մտցված մաթեմատիկական նշանակումների կիրառման օրինակներ:

Ցանկացած ռացիոնալ թիվ կարելի է ներկայացնել վերջավոր տասնորդական կամ անվերջ պարբերական տասնորդական կոտորակի տեսքով՝

$\begin{array}{l}\frac{7}{22}=\mathrm{0,3181818}...=\mathrm{0,3}(18)\\ 4=\mathrm{4,000}...=\mathrm{4,}(0)\\ \mathrm{7,3777}=\mathrm{7,37770000}...=\mathrm{7,3777}(0)\end{array}$

Ճիշտ է նաև հակառակ պնդումը՝ ցանկացած պարբերական տասնորդական կոտորակ ռացիոնալ թիվ է: 

Հաջորդ օրինակները ցույց են տալիս, թե ինչպես են պարբերական տասնորդական կոտորակները բերվում սովորական կոտորակների: