y=|x| ֆունկցիայի գրաֆիկն ու հատկությունները — դաս։ Հանրահաշիվ, 8-րդ դասարան.

Ցանկացած \(x\) իրական թվի համար կարելի է հաշվել նրա մոդուլը՝ \(|x|\) -ը: Սա նշանակում է որ կարելի է խոսել \(y = |x|\) ֆունկցիայի մասին:

Ունենք՝

y = \{\begin{cases} x, եթե x \geq 0 \\ x, եթե x < 0 \end{cases}

Կառուցենք այս ֆունկցիայի գրաֆիկը: Հարմար է գրաֆիկը կառուցել կտորներով:

Առաջին քայլ: Սկզբում կառուցենք \(y = x\) ուղիղը և առանձնացնենք նրա այն մասը, որը համապատասխանում է

x \in [0; + \infty)

արժեքներին (\(x\) -երի առանցքի դրական ճառագայթին):

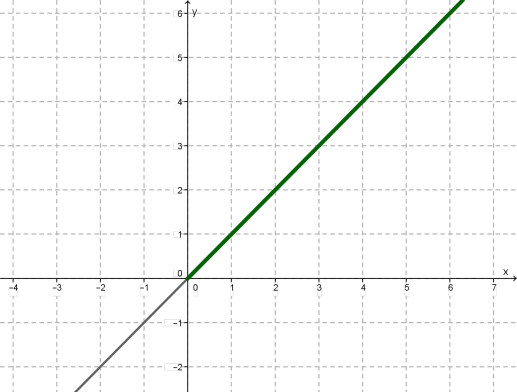
Երկրորդ քայլ: Հիմա կառուցենք \(y = -x\) ուղիղը և առանձնացնենք նրա այն մասը, որը համապատասխանում է

x \in (- \infty; 0)

արժեքներին (\(x\) -երի առանցքի բացասական ճառագայթին):

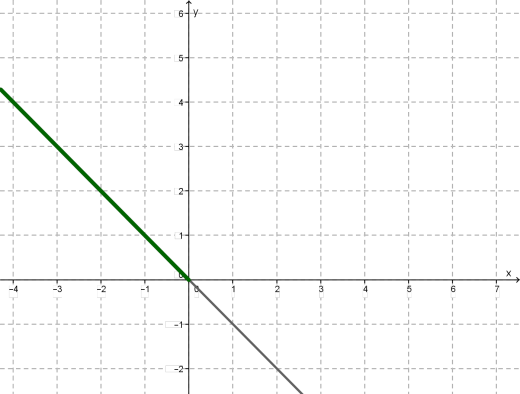
Երրորդ քայլ: Վերջապես, երկու կտորները նկարենք նույն կոորդինատական հարթության վրա: Ստանում ենք \(y = |x|\) ֆունկցիայի գրաֆիկը:

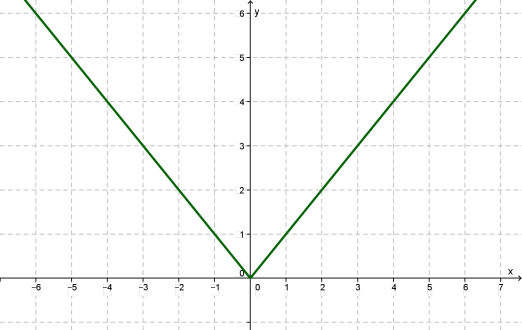
Թվարկենք գրաֆիկից բխող մի քանի հատկություններ:

1. Ֆունկցիան որոշված է ցանկացած կետում՝

D = (- \infty; + \infty)

2. Ցանկացած \(x\) -ի համար, \(|x|> 0\), բացի \(x = 0\) դեպքից և \(|0|= 0\)

3. Ֆունկցիան նվազում է

(- \infty; 0]

ճառագայթի վրա և աճում է

[0; + \infty)

ճառագայթի վրա:

4. Ֆունկցիան սահմանափակ չէ վերևից, բայց ներքևից սահմանափակ է:

5. Ֆունկցիան չունի մեծագույն արժեք, բայց ունի փոքրագույն արժեք՝ \(0\) -ն:

6. Ֆունկցիան անընդհատ է ամբողջ թվային առանցքի վրա՝

(- \infty; + \infty)

7. Ֆունկցիայի արժեքների բազմությունը օրդինատների առանցքի դրական ճառագայթն է՝

[0; + \infty)

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Սխա՞լ ես գտել

2. y=|x| ֆունկցիայի գրաֆիկն ու հատկությունները