
















Նշանի փոփոխման կանոնը
\(A\) և \(-A\) կոտորակները կոչվում են փոխադարձ հակադիր, եթե դրանց գումարը հավասար է \(0\)-ի, այսինքն՝ 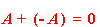
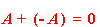
Հաճախ հանրահաշվական կոտորակների հետ գործողություններ կատարելիս, պետք է լինում փոխարինել կոտորակի համարիչը կամ հայտարարը հակադիրով: Սակայն, որպեսզի կոտորակի արժեքը չփոխվի, պետք է հետևել նշանի փոփոխության կանոններին՝
կոտորակի արժեքը չի փոխվի, եթե
- փոխենք համարիչի և հայտարարի նշանները,
- փոխենք համարիչի և ամբողջ կոտորակի նշանները,
- փոխենք հայտարարի և ամբողջ կոտորակի նշանները:
Եթե \(A\)-ով և \(B\)-ով նշանակենք հանրահաշվական կոտորակի համարիչն ու հայտարարը, ապա նշանի փոփոխման կանոնը կարելի է գրել հետևյալ կերպ՝
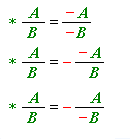
Կանոնը ուժի մեջ է միայն այն դեպքում, երբ 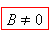
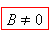
| 1) | 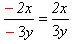 | - փոխված են համարիչի և հայտարարի նշանները |
| 2) | 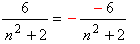 | - փոխված են համարիչի և ամբողջ կոտորակի նշանները |
| 3) | 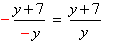 | - փոխված են համարիչի և ամբողջ
կոտորակի նշանները |
Այս հավասարությունները կարելի է ստուգել ցանկացած արժեքի համար հանրահաշվական կոտորակների որոշման տիրույթից:
ձևափոխությունը ճիշտ է \(m\)-ի ցանկացած արժեքի համար, բացի \(m = 0\)
Ստուգենք \(m = 1\) և \(m = 10\) դեպքերում:
Եթե \(m = 1\), ապա
Եթե \(m = 10\), ապա
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012: