Իրական թվերի կանոնները
1 -ին կանոն: Ցանկացած երկու և իրարից տարբեր իրական թվերից մեկը մյուսից մեծ է: Այսինքն, ցանկացած և իրական թվերի համար տեղի ունի հետևյալ առնչություններից միայն մեկը՝
Օրինակ
\(10\) և \(15\) թվերի համար ճիշտ է անհավասարությունը, և սխալ են մյուս երկու առնչությունները՝ և
2 -րդ կանոն: Ցանկացած երկու և իրարից տարբեր իրական թվերի միջև կա երրորդ թիվը: Այսինքն` եթե , ապա գոյություն ունի այնպիսի թիվ, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝
Օրինակ
\(1.4\) և \(1.5\) թվերի համար գոյություն ունի, օրինակ, \(1.44\) թիվը, այնպես, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝
3 -րդ կանոն: Ցանկացած երեք , և իրական թվերի համար, եթե և , ապա
Այս հատկությունը կոչվում է անհավասարությունների փոխանցելիության (տրանզիտիվության) հատկություն: Թվային առանցքի վրա կարելի է պատկերել այսպես:
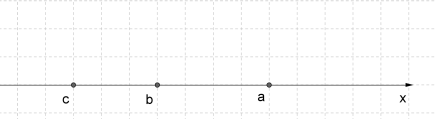
Օրինակ
և անհավասարություններից բխում է անհավասարությունը:
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012: