Ֆունկցիայի գրաֆիկի ուրվագծի կառուցումը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

\(y=f(x)\) ֆունկցիայի վարքի հետազոտման և գրաֆիկի ուրվագծի կառուցման համար, որպես կանոն, պետք է կատարել հետևյալ քայլերը:

1) Գտնել \(y=f(x)\) ֆունկցիայի \(D(f)\) որոշման տիրույթը:

2) Գտնել \(y=f(x)\) \(E(f)\) արժեքների բազմությունը:

3) Պարզել ֆունկցիայի պարբերականությունը:

4) Պարզել ֆունկցիայի զույգությունը:

5) Պարզել ֆունկցիայի սահմանափակությունը և գոյության դեպքում գտնել ֆոունկցիայի մեծագույն և փոքրագույն արժեքները:

6) Պարզել ֆունկցիայի անընդհատությունը կամ գտնել նրա խզման կետերը:

7) Գտնել ֆունկցիայի զրոները, մասնավորապես, որոշել ֆունկցիայի գրաֆիկի և կոորդինատային առանցքների հատման կետերը:

8) Գտնել ֆունկցիայի նշանապահպանման միջակայքերը:

9) Գտնել ֆունկցիայի մոնոտոնության միջակայքերը:

10) Գտնել ֆունկցիայի էքստրեմումի կետերն ու էքստրեմումները:

11) Եթե ֆունկցիայի որոշման տիրույթը բաղկացած է մեկ կամ մի քանի միջակայքերից, ապա պարզել ֆունկցիայի վարքը այդ միջակայքերի ծայրակետերում:

Կախված խնդրի պահանջից, վերը թվարկված քայլերի մի մասը կարելի է բաց թողնել կամ, եթե պահանջվում է գրաֆիկի մանրակրկիտ կառուցում, կատերել հավելյալ քայլեր (մասնավորապես, հաշվել ֆունկցիայի արժեքները որոշ կետերում և կազմել արժեքների աղյուսակ):

Քայլերի հերթականությունը պարտադիր չէ՝ այն կարելի է ընտրել նպատակահարմարությունից ելնելով:

Օրինակ

Կառուցենք

f (x) = \frac{3 x}{1 + |x|}

ֆունկցիայի գրաֆիկի ուրվագիծը:

1) Քանի որ կոտորակի հայտարարը զրո չի դառնում, ապա \(y=f(x)\) ֆունկցիայի որոշման տիրույթը ամբողջ թվային առանցքն է՝

D (f) = (- \infty; + \infty)

2) Նույն պատճառով, ֆունկցիան ամենուրեք անընդհատ է՝ խզման կետեր չունի:

3) Քանի որ

|f (x)| = \frac{3 |x|}{1 + |x|} < 3

ցանկացած \(x\)-ի համար (հայտարարը փոքրացրեցինք՝ \(1\)-ը \(0\)-ով փոխարինելով), ապա ֆունկցիան սահմանափակ է և՛ վերևից, և՛ ներքևից:

4) Հեշտ է տեսնել, որ

f (\pm 3) \neq 3

: Մյուս կողմից, եթե

x \to + \infty

, ապա ֆունկցիայի արժեքները անվերջ մոտենում են \(3\)-ին` \(3\)-ից փոքր մնալով, և

x \to - \infty

դեպքում՝ անվերջ մոտենում են \(-3\)-ին՝ \(-3\)-ից մեծ մնալով:

Հետևաբար, ֆունկցիան չունի փոքրագույն և մեծագույն արժեքներ և

E (f) = (- 3; 3)

5) Ֆունկցիան պարբերական չէ:

6) Ֆունկցիան կենտ է՝

f (- x) = - f (x)

7) Հեշտ է ստուգել, որ, եթե

x_{1}

\(<\)

x_{2}

, ապա տեղի ունի

f (x_{1}) < f (x_{2})

անհավասարությունը:

Հետևաբար, ֆունկցիան ամենուրեք խիստ աճում է, և ուրեմն, էքստրեմումի կետեր չունի:

8) Քանի որ \(y = 0)\) այն և միայն այն դեպքում, երբ \(x = 0\), ապա ֆունկցիայի գրաֆիկը կոորդինատային առանցքները հատում է միայն կոորդինատների սկզբնակետում:

f (x) = \frac{3 x}{1 + |x|}

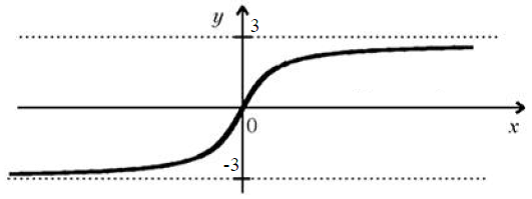
ֆունկցիայի գրաֆիկն ունի հետևյալ ուրվագիծը՝

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

2. Ֆունկցիայի գրաֆիկի ուրվագծի կառուցումը

Տեսություն