1. Գրաֆիկի կառուցման օրինակ

2) Քանի որ, \(f(-x) = f(x)\), ապա ֆունկցիան զույգ է, և բավական է նրա գրաֆիկը կառուցել ոչ բացասական \(x\)-երի համար: Բացասական \(x\)-երի համար գրաֆիկը կստացվի օրդինատների առանցքի նկատմամբ համաչափ արտապատկերման միջոցով:

 

3) Ֆունկցիան պարբերական չէ:

 

4) Ֆունկցիան սահմանափակ չէ ո՛չ վերևից, ո՛չ էլ ներքևից:

Հետևաբար, ֆունկցիան մեծագույն և ձոքրագույն արժեքներ չունի:

 

5) Ֆունկցիան խզվում է $x=\pm 3$ կետերում:

 

Ֆունկցիայի գրաֆիկը ստացվում է $y=\frac{1}{x}$ հիպերբոլի ձևափոխությունների միջոցով:

ա. Կառուցվում է $y=\frac{1}{\left|x\right|}$ ֆունկցիայի գրաֆիկը՝ բացասական \(x\)-երի համար հիպերբոլի ճյուղը համաչափ արտապատկերվում է աբսցիսների առանցքի նկատմամբ: 

բ. Կառուցվում է $y=\frac{1}{\left|x\right|-3}$ ֆունկցիայի գրաֆիկը՝ $y=\frac{1}{\left|x\right|}$ ֆունկցիայի գրաֆիկը տեղաշարժվում է \(3\) միավորով դեպի աջ:

գ. Կառուցվում է $y=\frac{2}{\left|x\right|-3}$ ֆունկցիայի գրաֆիկը՝ $y=\frac{1}{\left|x\right|-3}$ ֆունկցիայի գրաֆիկը \(2\) անգամ ձգվում է օրդինատների առանցքի երկայնքով՝ հեռանալով աբսցիսների առանցքից:

դ. Կառուցվում է $y=\frac{2}{\left|x\right|-3}+2$ ֆունկցիայի գրաֆիկը՝ $y=\frac{2}{\left|x\right|-3}$ ֆունկցիայի գրաֆիկը տեղաշարժվում է \(2\) միավորով դեպի վերև:

 

Ստանում ենք հետևյալ գրաֆիկը՝

 

 

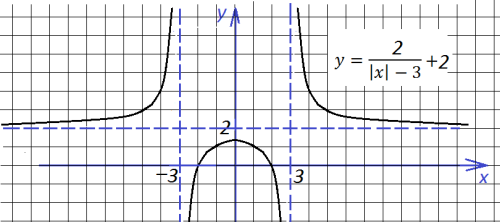
Հիմնվելով կառուցված գրաֆիկի և $y=\frac{1}{x}$ ֆունկցիայի ու նրա ձևափոխությունների հատկությունների վրա, շարունակենք թվարկել $y=\frac{2}{\left|x\right|-3}+2$ ֆունկցիայի հատկությունները:

 

6) Գտնենք ֆունկցիայի զրոները (հատումները աբսցիսների առանցքի հետ):

Լուծենք \(y = 0\) հավասարումը՝

Գտնենք հատումները օրդինատների առանցքի հետ՝ տեղադրելով \(x = 0\)`

$y\left(0\right)=-\frac{2}{3}+2=\frac{4}{3}$:

  

7) Ֆունկցիան նվազում է $[0;3)\text{ և }(3;+\mathrm{\infty })$ միջակայքերում և աճում է $(-\mathrm{\infty };-3)\text{ և }(-3;0]$ միջակայքերում:

 

8) Գտնենք ֆունկցիայի էքստրեմումի կետերը:

Ֆունկցիան մինիմումի կետ չունի, իսկ \(x = 0\)-ն ֆունկցիայի մաքսիմումի կետն է:

 

9) Գտնենք ֆունկցիայի էքստրեմումները:

Ֆունկցիան մինիմում չունի, իսկ մաքսիմումը $y_{\mathit{max}}=\frac{4}{3}$ արժեքն է:

10) Ֆունկցիան ընդունում է ցանկացած արժեք բացի \(y = 2\) արժեքից:

Այսինքն՝ ֆունկցիայի արժեքների բազմությունը $E(f)=\left(-\mathrm{\infty };2)\cup (2;+\mathrm{\infty }\right)$ բազմությունն է: