Եռանկյունաչափական ֆունկցիաների սահմանումը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Միավոր շրջանագծի վրա վերցնենք $B(x;y)$ կետը և դիտարկենք $OBD$ ուղղանկյուն եռանկյունը:

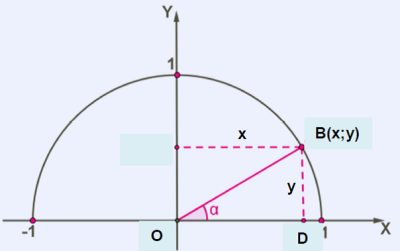
Երկրաչափության դասընթացից գիտենք, որ

\begin{array}{l} \sin α = \frac{BD}{OB} = \frac{y}{1}; \cos α = \frac{OD}{OB} = \frac{x}{1} \\ tg α = \frac{BD}{OD} = \frac{y}{x}; ctg α = \frac{OD}{BD} = \frac{x}{y} \end{array}

Այսպիսով՝

B (\cos α; \sin α)

\sin α

կոչվում է $B$ կետի $y$ կոորդինատը՝ օրդինատը:

\cos α

կոչվում է $B$ կետի $x$ կոորդինատը՝ աբսցիսը:

tg α

կոչվում է $B$ կետի օրդինատի հարաբերությունը աբսցիսին:

ctg α

կոչվում է $B$ կետի աբսցիսի հարաբերությունը օրդինատին

Սինուսը, կոսինուսը, տանգենսը և կոտանգենսը կոչվում են եռանկյունաչափական ֆունկցիաներ:

Միավոր շրջանագծի կամայական $B(x;y)$ կետի կոորդինատների համար տեղի ունեն հետևյալ անհավասարությունները՝

- 1 \leq x \leq 1; - 1 \leq y \leq 1

Հետևաբար, ցանկացած

α

անկյան սինուսը և կոսինուսը բավարարում են

- 1 \leq \cos α \leq 1; - 1 \leq \sin α \leq 1

անհավասարություններին:

Քանի որ միավոր շրջանագծի վրայով դրական կամ բացասական ուղղություններով լրիվ պտույտներ կատարելիս կետի դիրքը չի փոխվում, ապա՝

\begin{array}{l} \sin (α \pm 2 π) = \sin α; \cos (α \pm 2 π) = \cos α \\ tg (α \pm 2 π) = tg α; ctg (α \pm 2 π) = ctg α \end{array}

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. Եռանկյունաչափական ֆունկցիաների սահմանումը