2. Հավասարաչափ դանդաղող շարժում

Հավասարաչափ դանդաղող շարժման օրինակներ են արգելակող ինքնաթիռի, ուղղաձիգ դեպ վեր նետած մարմնի, թեք հարթությամբ դեպի վերև շարժվող մարմինների շարժումները (տե՛ս նկար):

 

 

Եթե արագացող շարժման դեպքում առաջնային խնդիրը մարմնի վերջնական արագությունը որոշելն էր, ապա արգելակելիս առաջնային է դառնում մինչև կանգ առնելը մարմնի անցած ճանապարհը որոշելու խնդիրը: Այդ խնդիրը լուծելու համար անհրաժեշտ է արագության և ճանապարհի բանաձևերը ստանալ դանդաղող շարժման դեպքում:

  

Այստեղից կստանանք արտահայտություն վերջնական արագության համար.

 

 

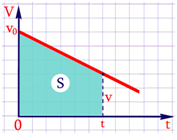
Արագությունը ժամանակից կախված է գծայնորեն, ուրեմն նրա գրաֆիկն ուղիղ գիծ է, որն արագության առանցքը հատում է $v_0$ կետում և թեքված է դեպի ժամանակի առանցքը.

Ճանապարհը գտնելու համար հաշվենք արագության գրաֆիկով սահմանափակված պատկերի մակերեսը.

 

 

որի մեջ կտեղադրենք արագության վերը նշված արտահայտությունը և կստանանք.

 

Արգելակման պահից սկսած՝ մարմնի արագությունը նվազում է: Մարմինը կանգ է առնում այն պահին, երբ արագությունը դառնում է զրո: Հետևաբար, արագության բանաձևից կունենանք $0=v_0-a{t}_0\Rightarrow v_0=a{t}_0$, այսինքն՝ արգելակման ժամանակը կարտահայտվի այսպես՝ $t_0=\frac{v_0}{a}$

Քանի որ կանգ առնելու պահին \(v = \)$v_0$,  \(t =\) $t_0$, ապա մարմնի անցած ճանապարհի բանաձևը կընդունի հետևյալ պարզ տեսքը՝ $S_0=\frac{v_0{t}_0}{2}$, որը արգելակման ճանապարհի բանաձևն է:

 

Հաշվի առնելով, որ անհավասարաչափ շարժման ճանապարհը՝ $S=v_{\text{միջ}}\cdot t$, ինչպես նաև այն, որ $v_0=a{t}_0$, կստանանք, որ արգելակման ժամանակ մինչև կանգ առնելը մարմնի անցած ճանապարհը կարելի է հաշվել նաև $S=\frac{a{t}^2}{2}$ բանաձևով: