Հավասարաչափ արագացող շարժում՝ արագացում, արագություն և ճանապարհ

Հավասարաչափ փոփոխական շարժումներ և դրանց դասակարգումը

Այն շարժումը, որի ժամանակ գոնե երկու հավասար ժամանակամիջոցներում մարմինն անցնում է անհավասար ճանապարհներ, կոչվում է անհավասարաչափ կամ փոփոխական շարժում:

Հիմնականում անհավասարաչափ են շարժվում գրեթե բոլոր մարմինները. փողոցում քայլող մարդը, սարից իջնող դահուկորդը, պատշգամբից ընկնող գնդակը, կանգառից հեռացող ավտոբուսը, վայրէջք կատարող ինքնաթիռը և այլն:

Ուշադրություն

Հավասարաչափ փոփոխական շարժում կատարող մարմնի արագությունը ժամանակի ընթացքում կարող է աճել (ինչպես ընկնող մարմնի արագությունը) կամ նվազել (ինչպես դեպի վեր նետած մարմնի արագությունը մինչև թռիչքի ամենաբարձր կետը հասնելը): Ըստ այդ հատկանիշի էլ հավասարաչափ փոփոխական շարժումները դասակարգում են երկու խմբի՝

ա) աճող արագությամբ հավասարաչափ փոփոխական շարժումներ, որոնց անվանում են հավասարաչափ արագացող:

բ) նվազող արագությամբ հավասարաչափ փոփոխական շարժումներ, որոնց անվանում են հավասարաչափ դանդաղող:

Հավասարաչափ արագացող շարժում, արագացում

Այն շարժումը, որի ընթացքում մարմնի արագությունը կամայական հավասար ժամանակամիջոցներում աճում է միևնույն չափով, կոչվում է հավասարաչափ արագացող շարժում:

Այն ֆիզիկական մեծությունը, որը հավասար է կամայական ժամանակամիջոցում արագության կրած փոփոխության և այդ ժամանակամիջոցի հարաբերությանը, կոչվում է հավասարաչափ արագացող շարժման արագացում:

Ուշադրություն

Արագացումն ընդունված է նշանակել $a$ տառով: Եթե հավասարաչափ փոփոխական շարժում կատարող մարմնի արագությունը $t$ ժամանակամիջոցում փոխվել է

Δ

$v$ -ով, ապա համաձայն սահմանման՝ մարմնի արագացումը կլինի

a = \frac{Δ v}{t}

Δ v = v_{2} - v_{1}

`ցանկացած ֆիզիկական մեծության համար վերջնական և սկզբնական արժեքների տարբերությունը կան փոփոխությունն ընդունված է նշանակել

Δ

-ով:

Եթե այս բանաձևի մեջ տեղադրենք $t = 1$ վ, ապա կստանանք, որ արագացման մեծությունը հավասար է արագության փոփոխությանը $a =$

Δ

$v$, այսինքն`արագացումը իրոք ցույց է տալիս արագության կրած փոփոխությունը միավոր ժամանակում:

Միավորների ՄՀ -ում արագացման միավորը 1 $մ / վ^{2}$ -ն է: Դա այն մարմնի արագացումն է, որի արագությունը յուրաքանչյուր վայրկյանում փոխվում է $1$ մ/վ -ով։

Հավասարաչափ փոփոխական շարժում կատարող մարմնի արագությունը ժամանակի ընթացքում կարող է աճել (ինչպես, օրինակ այն դեպքում երբ մարմինն ընկնում է, կամ գլորվում է թեք հարթությամբ ներքև շարժման դեպքում, նկ. 1), կամ նվազել (ինչպես, օրինակ, դեպի վեր նետված կամ թեք հարթությամբ դեպի վեր գլորած գնդակի շարժման դեպքում, նկ. 2): Ըստ այդ հատկանիշի էլ հավասարաչափ փոփոխական շարժումները դասակարգում են երկու խմբի՝

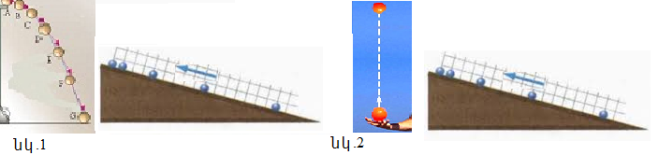
ա) աճող արագությամբ հավասարաչափ փոփոխական շարժումներ, որոնց անվանում են հավասարաչափ արագացող,

բ) նվազող արագությամբ հավասարաչափ փոփոխական շարժումներ, որոնց անվանում են հավասարաչափ դանդաղող:

Հավասարաչափ փոփոխական շարժման արագացման վեկտորը

Մարմնի արագացումը արագության նման բնութագրվում է ոչ միայն թվային արժեքով, այլև ուղղությամբ։ Դա նշանակում է, որ արագացումը նույնպես վեկտորական մեծություն է։ Այդ պատճառով նկարներում այն պատկերվում է սլաքով։

Հավասարաչափ արագացող շարժման դեպքում արագացումն ուղղված է շարժման ուղղությամբ (տե՛ս նկար 3 ա), իսկ դանդաղող շարժման դեպքում`շարժման հակառակ ուղղությամբ (տե՛ս նկար 3 բ),

Արագությունը և ճանապարհը հավասարաչափ արագացող շարժման դեպքում

Դիտարկենք հավասարաչափ արագացող շարժման երկու դեպք, երբ այն սկսվում է դադարի վիճակից (մասնավոր դեպք), և երբ ժամանակի հաշվարկման սկզբնապահին այն ունի որոշակի արագություն (ընդհանուր դեպք):

1. Հավասարաչափ արագացող շարժում դադարի վիճակից

Դադարի վիճակից սկսվող շարժումների մեծ մասը սկզբում հավասարաչափ արագացող են: Հավասարաչափ արագացող շարժում են կատարում թռիչքուղի դուրս եկած ինքնաթիռը, կայարանից շարժվող գնացքը, կանգառից շարժվող ավտոբուսը, լուսացույցի տակ կանգնած ավտոմեքենան՝ կանաչ լույսը վառվելուց հետո, տարբեր մրցումների մասնակիցները մրցավազքի սկիզբը ազդարարող ազդանշանից հետո և այլն:

Որպեսզի շարժվող ինքնաթիռը թռիչքի պատրաստվելիս կարողանա գետնից վեր բարձրանալ, անհրաժեշտ է, որ նրա արագությունը մեծանա մինչև որոշակի արժեքի և դա պետք է անել մինչև թռիչքուղու վերջին հասնելը: Ուստի թռիչքը կառավարելու համար շատ կարևոր է իմանալ հավասարաչափ արագացող շարժման առանձնահատկությունները. թե ինչ արագացմամբ պետք է թափավազք կատարի ինքնաթիռը, ինչպես պետք է աճի նրա արագությունը, որպեսզի մինչև թռիչքուղու ավարտը հասնի անհրաժեշտ արժեքին:

Դիցուք դադարի վիճակից հավասարաչափ արագացող շարժում կատարող մարմնի արագությունը շարժման սկզբից $t$ ժամանակ անց դարձել է $v$: Այդ դեպքում նրա արագության փոփոխությունը՝

Δ

$v$: Տեղադրելով

Δ

$v$-ի այս արժեքը, կարող ենք գտնել մարմնի արագության կախումը ժամանակից՝ $v = at$:

Դադարի վիճակից հավասարաչափ արագացող շարժում կատարող մարմնի ճանապարհը կարելի է հաշվել $S = \frac{a t^{2}}{2}; S = \frac{v^{2}}{2 a}$ բանաձևով:

$v = at$ բանաձևը կապ է ստեղծում արագության, արագացման և շարժման ժամանակների միջև: $S$-ի համար ստացված $S = \frac{v^{2}}{2 a}$ առնչությունից ստացվում է $v = \sqrt{2 aS}$ բանաձևը:

2. Սկզբնական արագությամբ հավասարաչափ արագացող շարժում

Եթե հավասարաչափ արագացող շարժման սկզբում մարմինն ունեցել է $v_{0}$ սկզբնական արագություն, ապա մինչև ժամանակի $t$ պահը արագության փոփոխությունը՝ $Δ$ $v = v – $ $v_{0}$ , այդ դեպքում.

a = \frac{v - v_{0}}{t}

Այստեղից կստանանք

v = v_{0} + at

Բանաձևը ցույց է տալիս, որ արագության գրաֆիկն ուղիղ գիծ է, որն ստացվում է նկարում պատկերված գրաֆիկը օրդինատների առանցքով \(v

0\) միավորով դեպի վեր զուգահեռ տեղափոխելով: Այս դեպքում շարժման սկզբից մինչև ժամանակի կամայական $t$ պահը մարմնի արագության գրաֆիկով սահմանափակված պատկերը սեղան է, որի մեծ հիմքը $v$ է, փոքրը՝ $v0$, իսկ բարձրությունը՝ $t$: Հետևաբար, այդ պատկերի մակերեսը, ուստի նաև $t$ ժամանակում մարմնի անցած ճանապարհը՝

S = v_{0} t + \frac{a t^{2}}{2}

Աղբյուրները

Ս. Վ. Գրոմով , Ն. Ա. Ռոդինա, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք ( I, II, III և V գլուխների հեղինակ Ա. Մամյան); Երևան, Անտարես -2014 թ.

Է. Ղազարյան, Ա. Կիրակոսյան, Գ. Մելիքյան, Ռ. Թոսունյան, Ս. Մաիլյան, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք; Երևան, Էդիտ Պրինտ -2008 թ

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Հավասարաչափ արագացող շարժում՝ արագացում, արագություն և ճանապարհ

Տեսություն