Նյուտոնի երրորդ օրենքը

Օրինակ

Երբ դադարի վիճակում գտնվող սայլակների միջև դրված ճկուն թիթեղը կապող թելը կտրում են (տե՛ս նկար), փոխազդեցության հետևանքով նրանք ձեռք են բերում որոշակի արագություններ, որոնք զանգվածների հետ կապված են

m_{1} v_{1} = m_{2} v_{2}

առնչությամբ: Եթե սայլակների փոխազդեցության տևողությունը նշանակենք $t$ -ով, իսկ այդ ընթացքում նրանց արագացումները համապատասխանաբար՝

a_{1}

–ով և

a_{2}

-ով, ապա քանի որ

v_{1} = a_{1} t

v_{2} = a_{2} t

, ուստի

m_{1} a_{1} t = m_{2} a_{2} t

, որտեղից՝

m_{1} a_{1} = m_{2} a_{2}

: Համաձայն Նյուտոնի երկրորդ օրենքի՝

{m_{1} a_{1} = F}_{1}

{m_{2} a_{2} = F}_{2}

, հետևաբար՝ ուժերի մոդուլները հավասար են`

F_{1} = F_{2}

Փոխազդեցության հետևանքով առաջին սայլակը սկսում է շարժվել դեպի ձախ, իսկ երկրորդը՝ դեպի աջ: Սա էլ նշանակում է, որ սայլակները միմյանց վրա ազդում են ուղղությամբ հակադիր ուժերով:

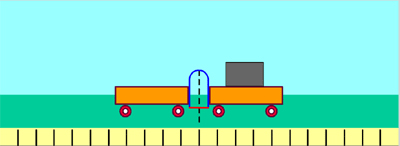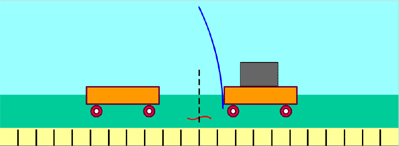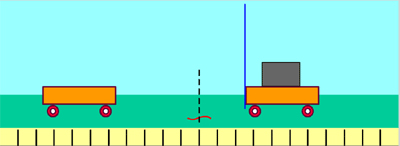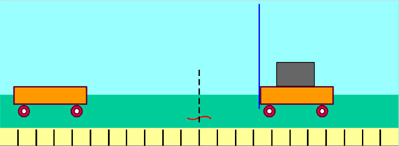
Այս եզրակացության ճշմարտացիության մեջ կարելի է համոզվել նաև հետևյալ պարզ փորձով: Կեռիկներով իրար միացված ուժաչափերից ամրացված պարանները ձգենք հակադիր ուղղություններով (տե՛ս նկար): Կտեսնենք, որ ուժաչափերի ցուցմունքները համընկնում են: Նշանակում է՝ ինչ ուժով որ առաջին ուժաչափն ազդում է երկրորդի վրա, նույն ուժով երկրորդն է ազդում առաջինի վրա:

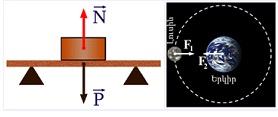
Հորիզոնական հենարանի վրա դրված մարմնի և հենարանի փոխազդեցության հետևանքով և՛ մարմինը, և՛ հենարանը դեֆորմացվում են (տե՛ս նկար): Դրա հետևանքով մարմնում առաջացած առաձգականության ուժով այն ազդում է հենարանի վրա (մարմնի կշիռ): Հենարանն իր հերթին առաձգականության ուժով ազդում է մարմնի վրա, որն ուղղված է ուղղաձիգ դեպի վեր ($N$՝ հակազդեցության ուժ):

Ուշադրություն

Ուստի ասում են, որ հակազդեցության ուժը և կշիռը նույն բնույթի (առաձգական) ուժեր են: Դրանք ուղղությամբ հակադիր են, մեծությամբ՝ հավասար $P = N$

Նույնը կարելի է ասել տիեզերական ձգողության մասին: Տիեզերական ձգողության օրենքից հետևում է, որ Երկիրը և Լուսինը միմյանց ձգում են $F_{1} = F_{2} = G \frac{M_{Ե} m_{լ}}{r^{2}}$ ուժով, որտեղ $G$-ն գրավիտացիոն հաստատունն է, $M_{Ե} {, m}_{լ}$ -ը՝ Երկրի և Լուսնի զանգվածները, $r$-ը՝ նրանց կենտրոնների հեռավորությունը (տե՛ս նկար): Ուրեմն Երկիրն ու Լուսինն էլ են փոխազդում նույն բնույթի (գրավիտացիոն) ուժերով, որոնք ուղղությամբ հակադիր են, մեծությամբ` հավասար:

images (25).jpg

Միավորելով փորձերի արդյունքները և տարածելով դրանք բոլոր մարմիններ փոխազդեցության վրա՝ հանգում ենք Նյուտոնի երրորդ օրենքին.

Մարմինները միմյանց հետ փոխազդում են նույն բնույթի` մոդուլով հավասար և ուղղությամբ հակադիր ուժերով:

Մաթեմատիկորեն Նյուտոնի երրորդ օրենքը ներկայացվում է այսպես՝

{\vec{F}}_{12} = - {\vec{F}}_{21}

որտեղ

{\vec{F}}_{12}

-ը առաջին մարմնի վրա երկրորդի կողմից ազդող ուժն է,

{\vec{F}}_{21}

-ը՝ երկրորդի վրա առաջինի կողմից ազդող ուժը: $«-»$ նշանը ցույց է տալիս, որ այդ ուժերն ունեն հակադիր ուղղություններ:

Ուշադրություն

Նյուտոնի երրորդ օրենքը ցույց է տալիս, որ մարմինների փոխազդեցության հետևանքով ուժերը միշտ հանդես են գալիս զույգերով: Եթե մի մարմինն ազդում է այլ մարմնի վրա, ապա վերջինս նրան հակազդում է նույնպիսի, բայց հակառակ կողմ ուղղված ուժով:
Նյուտոնի երրորդ օրենքը կիրառելիս միշտ պետք է հիշել, որ մարմինների փոխազդեցության ուժերը կիրառված են տարբեր մարմինների վրա, ուստի այդ ուժերը միմյանց հավասարակշռել չեն կարող:

Հաճախ հանդիպող հարց

Նյուտոնի երրորդ օրենքից բխում է, որ ինչ ուժով մարդը քաշում է սահնակը, նույն ուժով սահնակը նրան հետ է քաշում (տե՛ս նկարը): Բայց սահնակն առաջ է շարժվում, իսկ մարդը հետ չի շարժվում: Ինչպե՞ս բացատրել այս երևույթը: Բանն այն է, որ մարդը և սահնակը, պարանի միջոցով միմյանց հետ փոխազդելուց բացի, փոխազդում են նաև Երկրի հետ: Երբ մարդը հրվում է գետնից (թեկուզ և ձյունածածկ), վերջինս ազդում է նրա վրա մի ուժով, որն ավելի մեծ է, քան սահնակի կողմից ազդող ուժը, ուստի նա շարժվում է առաջ: Եթե մարդը սահնակը քաշեր ոչ թե ձյան, այլ բացարձակ հարթ մերկասառույցի վրա, ապա նա իրոք հետ կշարժվեր, իսկ սահնակը՝ առաջ, մինչև որ նրանք կհանդիպեին իրար:

Աղբյուրները

Ս. Վ. Գրոմով , Ն. Ա. Ռոդինա, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք ( I, II, III և V գլուխների հեղինակ Ա. Մամյան); Երևան, Անտարես -2014 թ.

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

3. Նյուտոնի երրորդ օրենքը

Տեսություն