Վեկտորի կոորդինատները — դաս։ Երկրաչափություն, 9-րդ դասարան.

Վեկտորի կոորդինատները

Վեկտորը, որի երկարությունը հավասար է հատվածների չափման միավորին, անվանում են միավոր վեկտոր:

O (0; 0)

կետից տեղադրված, կոորդինատների առանցքների դրական ուղղություններն ունեցող

\vec{i}

\vec{j}

վեկտորները կոչվում են կոորդինատային վեկտորներ:

\vec{i}

-ն աբսցիսների առանցքի վրա է, իսկ

\vec{j}

-ն՝ օրդինատների (տես ներքևի նկարը):

\vec{i}

\vec{j}

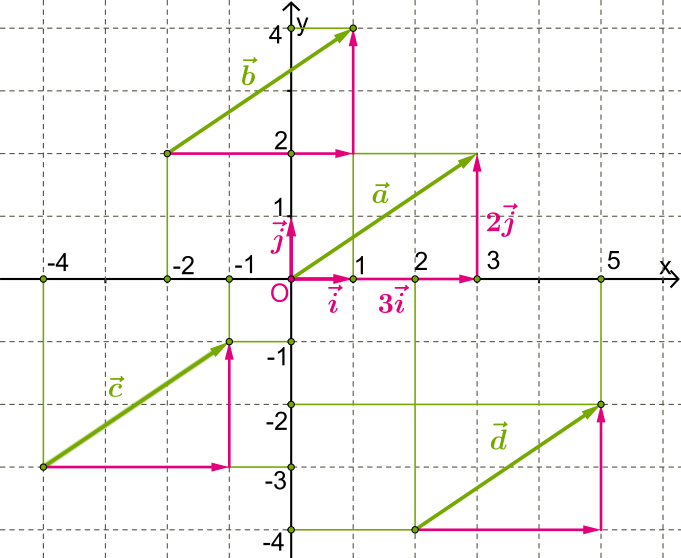
կոորդինատային վեկտորները տարագիծ են:

Հետևաբար, ցանկացած վեկտոր կարելի է վերածել՝ ըստ կոորդինատային վեկտորների:

Վերևի նկարում

\vec{a}

վեկտորի վերածումն ըստ

\vec{i}

\vec{j}

վեկտորների ունի հետևյալ տեսքը՝

\vec{a} = 3 \cdot \vec{i} + 2 \cdot \vec{j}

\vec{a}

վեկտորի՝ ըստ կոորդինատային վեկտորների վերածման գործակիցները կոչվում են

\vec{a}

վեկտորի կոորդինատներ:

Մենք արդեն ծանոթ ենք վեկտորի կոորդինատներին:

Ինչպես գիտենք, վեկտորի կոորդինատները գտնելու համար այն պետք է տեղադրել

O (0; 0)

կետում: Վեկտորի կոորդինատները կլինեն վերջնակետի կոորդինատները:

Տեսնում ենք, որ դրանք հենց վերածման գործակիցներն են:

Գրում ենք այսպես՝

\vec{a} \{3; 2\}

Քանի որ, ըստ տարագիծ վեկտորների վերլուծման գործակիցները միակն են, ապա՝

1) հավասար վեկտորների կոորդինատները հավասար են

2) հակադիր վեկտորների կոորդինատները հակադիր թվեր են

Այսպիսով, հակադիր վեկտորի կոորդինատները ստանալու համար պետք է վեկտորի կոորդինատները բազմապատկել \(-1\)-ով:

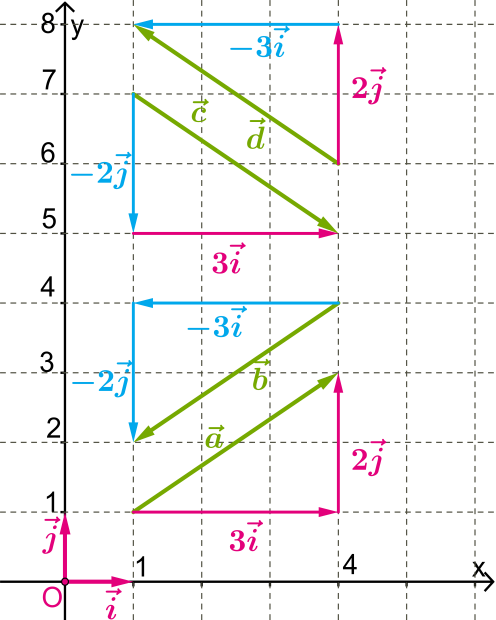
Հիշենք որ, վեկտորի կոորդինատները հավասար են նրա վերջնակետի և սկզբնակետի կոորդինատների տարբերությանը:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013:

Սխա՞լ ես գտել

1. Վեկտորի կոորդինատները