
















Կառուցման խնդիրներ

Խնդիրներում, որոնցում պետք է կատարել կառուցումներ, օգտագործում են կարկին և քանոն:
Շատ կարևոր է հիշել, որ այդ խնդիրներում քանոնը օգտագործվում է ոչ թե որպես չափման գործիք, այլ բացառապես տրված երկու կետերով ուղիղ, ճառագայթ կամ հատված գծելու համար: Կարկինը օգտագործվում է շրջանագիծ և շրջանագծի աղեղ կառուցելու համար:
Դիտարկենք հինգ հիմնական կառուցումները, որոնցում օգտագործում ենք նշված գործողությունները՝ ուղիղ գծի և շրջանագծի կառուցումը:
\(1\). Տրված ճառագայթի վրա սկզբնակետից տեղադրել տրված հատվածին հավասար հատված:
\(2\). Կառուցել տրված անկյանը հավասար անկյուն:
\(3\). Կառուցել անկյան կիսորդը:
\(4\). Կառուցել փոխուղղահայաց ուղիղներ:
\(5\). Կառուցել հատվածի միջնակետը:
\(1\). Տրված ճառագայթի վրա սկզբնակետից տեղադրել տրված հատվածին հավասար հատված:
Դիտիր տեսանյութը:
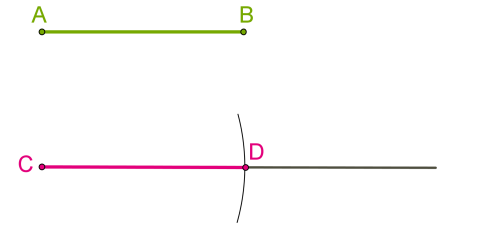
Պարզ է, որ այս եղանակով մենք ստանում ենք տրվածին հավասար հատված: Ըստ սահմանման՝ շրջանագիծը բաղկացած է կետերից, որոնք գտնվում են որոշ կետից (շրջանագծի կենտրոն) միևնույն հեռավորության (շառավիղ) վրա:
Եթե կենտրոնը ճառագայթի \(C\) սկզբնակետն է, իսկ շառավիղը տրված \(AB\) հատվածը, ապա շրջանագծի և ճառագայթի հատման \(D\) կետը հենց տրված \(AB\) հատվածին հավասար \(CD\) հատվածի ծայրակետն է:
\(2\). Տրված անկյանը հավասար անկյան կառուցումը:
Դիտիր տեսանյութը:
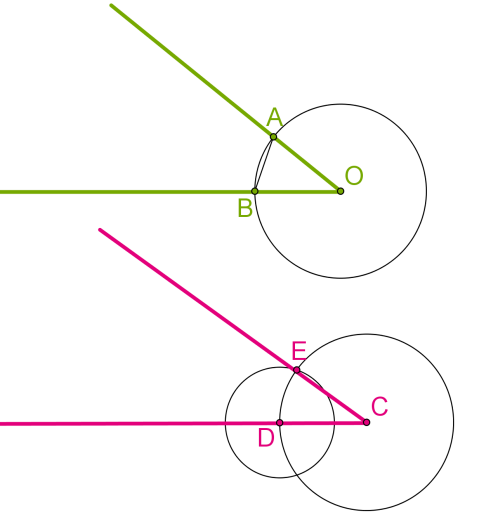
Ապացուցենք, որ կառուցված \(ECD\) անկյունը, իրոք, հավասար է տրված \(AOB\) անկյանը:
Կառուցենք ճառագայթի սկզբնակետում գտնվող \(C\) կենտրոնով շրջանագիծ, որի շառավիղը հավասար է \(O\) կենտրոնով շրջանագծի շառավղին: Ապա՝ \(CD\)\(=\)\(OB\):
Եթե մենք կառուցել ենք \(D\) կենտրոնով և \(BA\)-ին հավասար շառավղով շրջանագիծ, ապա այն հատում է նախորդ շրջանագիծը \(E\) կետում, ընդ որում՝ \(BA\)\(=\)\(DE\):
Տանենք \(CE\) ճառագայթը: Ակնհայտ է, որ \(OA\)\(=\)\(CE\):
Հետևաբար, ըստ եռանկյունների հավասարության երրորդ հայտանիշի, \(AOB\) և \(ECD\) եռանկյունները հավասար են: Ուրեմն հավասար են նաև դրանց համապատասխան անկյունները, մասնավորապես՝ \(ECD\) անկյունը հավասար է տրված \(AOB\) անկյանը:
\(3\). Անկյան կիսորդի կառուցումը:
Դիտիր տեսանյութը:
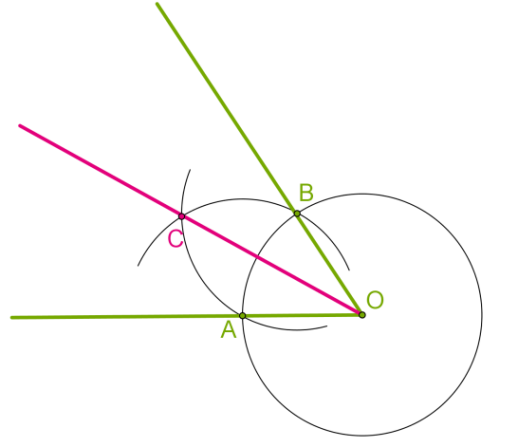
Որպեսզի համոզվենք, որ \(OC\)-ն իրոք բաժանում է \(AOB\) անկյունը հավասար մասերի, բավական է դիտարկել \(AOC\) և \(BOC\) եռանկյունները:
\(OA = OB\) որպես նույն շրջանագծի շառավիղներ, իսկ \(AC = BC\), քանի որ կառուցման ընթացքում, երկու շրջանագծերի համար մենք ընտրեցինք նույն շառավիղները:
\(OC\) կողմը ընդհանուր է:
Այդ եռանկյունները հավասար են՝ ըստ եռանկյունների հավասարության երրորդ հայտանիշի:
Հետևաբար դրանց համապատասխան անկյունները հավասար են:
Այսպիսով, \(AOC\)-ն և \(BOC\)-ն մեկ անկյան երկու հավասար մասեր են, ինչը նշանակում է, որ \(OC\) ճառագայթը, իրոք, անկյունը բաժանում է երկու հավասար մասերի:
\(4\). Փոխուղղահայաց ուղիղների կառուցումը:
Դիտիր տեսանյութը:
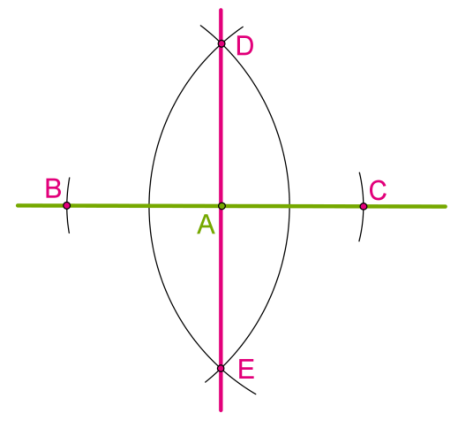
Ինչո՞ւ է \(DE\)-ն ուղղահայաց \(BC\)-ին:
\(AB = AC\)՝ այդպես են այդ կետերը վերցրել կառուցման ընթացքում:
\(BD = CD\), քանի որ մենք երկու շրջանագծերը կառուցեցինք նույն շառավղով:
Հետևաբար \(DA\)-ն և \(EA\)-ն \(ADB\) և \(AEB\) հավասարասրուն եռանկյունների հիմքերի միջնագծերն են:
Հավասարասրուն եռանկյան միջնագիծը նաև նրա բարձրությունն է, ուրեմն, ուղղահայաց է հիմքին:
\(5\). Հատվածի միջնակետի կառուցումը:
Դիտիր տեսանյութը:
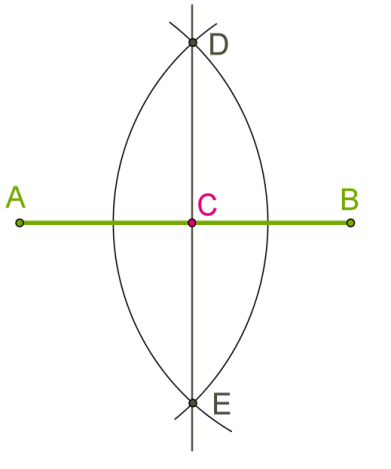
Այս կառուցումը համընկնում է փոխուղղահայաց ուղիղների կառուցման հետ: Արդեն ապացուցված է, որ \(DC\)-ն կամ \(EC\)-ն բաժանում են \(AB\) հատվածը երկու հավասար մասերի: Ուրեմն, \(C\) կետը \(AB\) հատվածի միջնակետն է:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ.Կադոմցեվ, Է.Գ.Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: