
















Եռանկյան կառուցումն ըստ երեք տարրերի
Մենք արդեն դիտարկել ենք կառուցման հետևյալ խնդիրները.
\(1\). Տրված ճառագայթի վրա սկզբնակետից տեղադրել տրված հատվածին հավասար հատված:
\(2\). Կառուցել տրված անկյանը հավասար անկյուն:
\(3\). Կառուցել անկյան կիսորդը:
\(4\). Կառուցել փոխուղղահայաց ուղիղներ:
\(5\). Կառուցել հատվածի միջնակետը:
Օգտագործելով դիտարկված խնդիրները և եռանկյան տրված տարրերը` կարելի է կառուցել տրվածին հավասար եռանկյուն:
Օրինակ
Եռանկյան կառուցումն՝ ըստ տրված երկու կողմերի և նրանցով կազմված անկյան:
Տրված են երկու հատվածներ՝ \(a\) և \(b\), որոնք հավասար են տրված եռանկյան կողմերին և \(1\)-ը, որը հավասար է տրված եռանկյան կողմերով կազմված անկյանը: Պահանջվում է կառուցել եռանկյուն, որի տարրերը հավասար են տրված հատվածներին և անկյանը:
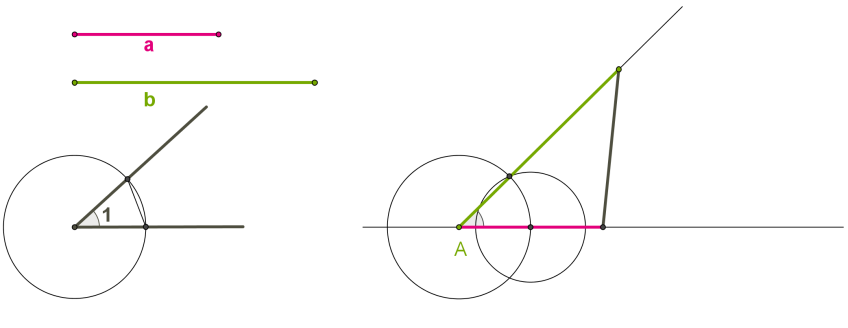
1. Տանել ուղիղ:
2. Ուղղի վրա \(A\) կետից տեղադրել հատված, որը հավասար է տրված \(a\) հատվածին:
3. Կառուցել տրված \(1\) անկյանը հավասար անկյուն (անկյան գագաթը պետք է լինի \(A\) կետը, և անկյան մի կողմը պետք է ընկած լինի ուղղի վրա):
4. Անկյան մյուս կողմի վրա տեղադրել տրված \(b\) հատվածին հավասար հատված:
5. Միացնել հատվածների ծայրակետերը:
Եռանկյունների հավասարության առաջին հայտանիշի հիման վրա եզրակացնում ենք, որ կառուցված եռանկյունը հավասար է տրված եռանկյանը:
Օրինակ
Եռանկյան կառուցումը ըստ կողմի և նրան առընթեր երկու անկյունների:
Տրված է \(a\) հատվածը և երկու անկյուններ՝ \(1\) և \(2\), որոնք հավասար են տրված եռանկյան կողմին առընթեր անկյուններին: Պահանջվում է կառուցել եռանկյուն, որի տարրերը հավասար են տրված հատվածին և անկյուններին:
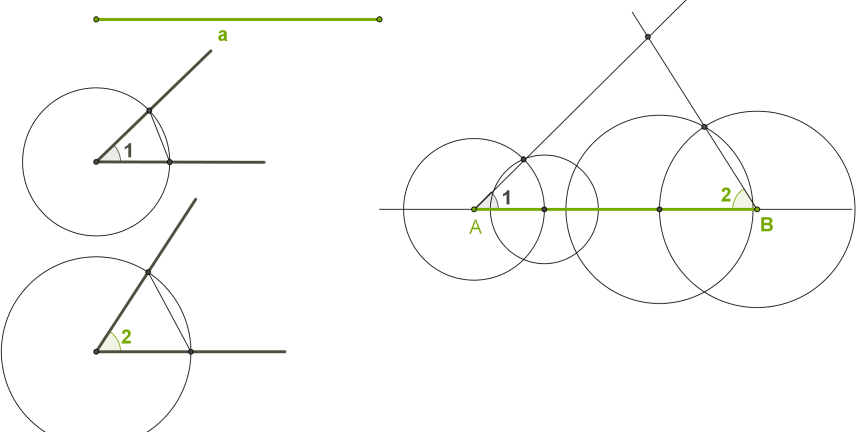
1. Տանել ուղիղ:
2. Ուղղի վրա \(A\) կետից տեղադրել տրված \(a\) հատվածին հավասար հատված և \(B\)-ով նշանակել հատվածի մյուս ծայրակետը:
3. Կառուցել տրված \(1\) անկյանը հավասար անկյուն (անկյան գագաթը պետք է լինի \(A\) կետը, և անկյան մի կողմը պետք է ընկած լինի ուղղի վրա):
4. Կառուցել տրված \(2\) անկյանը հավասար անկյուն (անկյան գագաթը պետք է լինի \(B\) կետը, և անկյան մի կողմը պետք է ընկած լինի ուղղի վրա):
5. Անկյունների մյուս կողմերի հատման կետը կլինի պահանջվող եռանկյան երրորդ գագաթը:
Եռանկյունների հավասարության երկրորդ հայտանիշի հիման վրա եզրակացնում ենք, որ կառուցված եռանկյունը հավասար է տրված եռանկյանը:
Օրինակ
Եռանկյան կառուցումն` ըստ երեք կողմերի
Տրված են երեք հատվածներ՝ \(a\),\(b\) և \(c\), որոնք հավասար են տրված եռանկյան երեք կողմերին: Պահանջվում է կառուցել եռանկյուն, որի կողմերը հավասար են տրված հատվածներին:
Այս դեպքում, մինչև կառուցումը պետք է համոզվել, որ տրված կողմերով եռանկյուն գոյություն ունի: Դա կարելի է անել՝ ստուգելով եռանկյան անհավասարությունը (յուրաքանչյուր հատվածի երկարությունը պետք է փոքր լինի մյուս երկուսի գումարից):
Եթե այո, ապա՝
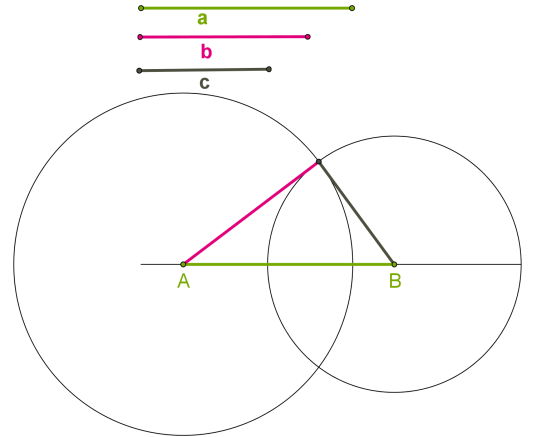
1. Տանել ուղիղ:
2. Ուղղի վրա \(A\) կետից տեղադրել տրված \(a\) հատվածին հավասար հատված և \(B\)-ով նշանակել հատվածի մյուս ծայրակետը:
4. Տանել \(B\) կենտրոնով և \(c\) հատվածին հավասար շառավղով շրջանագիծ:
5. Շրջանագծերի հատման կետը կլինի պահանջվող եռանկյան երրորդ գագաթը:
Եռանկյունների հավասարության երրորդ հայտանիշի հիման վրա եզրակացնում ենք, որ կառուցված եռանկյունը հավասար է տրված կողմերով եռանկյանը:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ.Կադոմցեվ, Է.Գ.Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: