
















Աքսիոմների հետևանքներ
1. Ուղղով և նրա վրա չգտնվող կետով կարելի է տանել հարթություն և այն էլ՝ միայն մեկը:
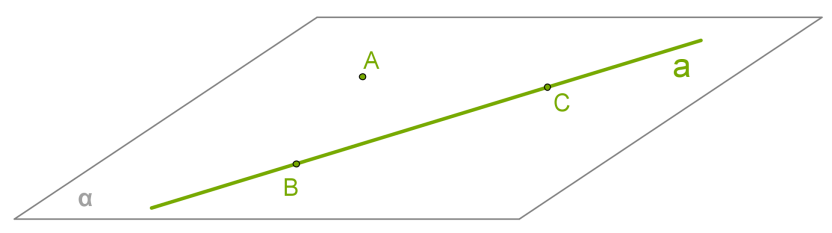
Ապացուցում:
1) Դիտարկենք \(a\) ուղիղը և նրա վրա չգտնվող \(A\) կետը:
2) \(a\) ուղղի վրա վերցնենք \(B\) և \(C\) կետերը:
3) Քանի որ երեք կետերը ընկած չեն նույն հարթության մեջ, ապա երկրորդ աքսիոմից հետևում է, որ \(A\), \(B\), \(C\) կետերով կարելի է տանել միակ հարթությունը:
4) \(a\) ուղղի \(B\) և \(C\) կետերը ընկած են ուղղի վրա, ուստի, երրորդ աքսիոմից հետևում է, որ հարթությունը անցնում է \(a\) ուղղով և \(A\) կետով:
2. Երկու հատվող ուղիղներով կարելի է տանել հարթություն և այն էլ՝ միայն մեկը:
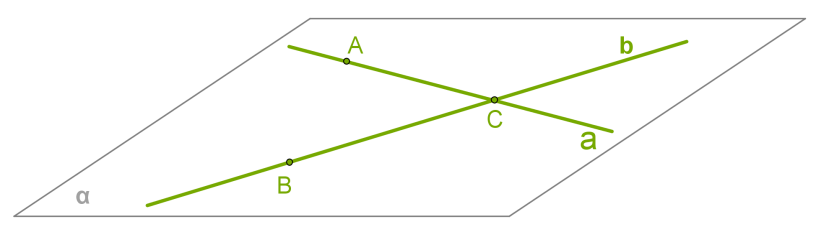
Ապացուցում:
1) Դիտարկենք \(a\) և \(b\) ուղիղները, որոնք հատվում են \(C\) կետում:
2) \(a\) ուղղի վրա վերցնենք \(A\) կետը, իսկ \(b\) ուղղի վրա՝ \(B\) կետը այնպես, որ ընտրված կետերը չհամընկնեն \(C\) կետի հետ:
3) Երրորդ աքսիոմի հիման վրա \(A\), \(B\) և \(C\) կետերով կարելի է տանել հարթությունը: Այդ դեպքում \(a\) և \(b\) ուղիղները գտնվում են հարթության մեջ (ըստ երրորդ աքսիոմի):
Օրինակ
Տրված են \(AC\) և \(BD\) հատվող հատվածները: Ապացուցենք, որ \(AB\), \(BC\), \(CD\), \(DA\) հատվածները գտնվում են միևնույն հարթության մեջ:
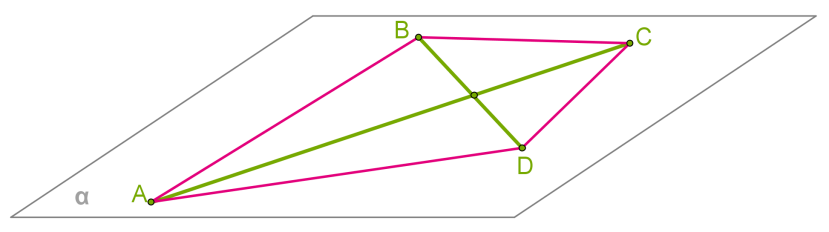
Լուծում:
1) Երկրորդ աքսիոմից հետևում է, որ \(AC\) և \(BD\) հատվածներով կարելի է տանել միակ ուղիղը, որը նշանակենք -ով: Հետևաբար, \(A, B, C\) և \(D\) կետերը գտնվում են հարթության մեջ:
2) Երրորդ աքսիոմից հետևում է, որ \(AB\), \(BC\), \(CD\) և \(DA\) հատվածների բոլոր կետերը ընկած են միևնույն հարթության մեջ: Հետևաբար, բոլոր չորս հատվածները ընկած են մեջ:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009