
















Տարածական պատկեր և տարածական մարմին
Այն պատկերը, որի ոչ բոլոր կետերն են ընկած միևնույն հարթության մեջ, կոչվում է տարածական պատկեր:
Տարածության սահմանափակված մասը կոչվում է երկրաչափական կամ տարածաչափական մարմին, իսկ մարմինը սահմանափակող կետերի բազմությունը՝ մարմնի մակերևույթ:
Գունդը երկրաչափական մարմին է, գնդոլորտը նրա մակերևույթն է:
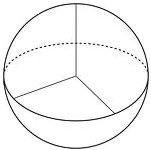 գունդ |  գնդոլորտ |
Պարուրաձև գիծը տարածական պատկեր է: Սակայն այն մարմին չէ:
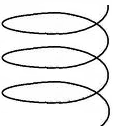
պարուրաձև գիծ
Բուրգը երկրաչափական մարմին է, որը սահմանափակված է բազմանկյուններով:
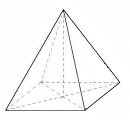 բուրգ | 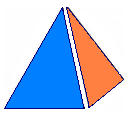 հարթ բազմանկյուններ |
Հարթություն
Հարթությունը պարզագույն մակերևույթ է: Շրջակա միջավայրում շատ առարկաներ հարթություն են հիշեցնում, օրինակ՝ սենյակի հատակը, սեղանը, լողավազանի կամ լճի ջրի մակերևույթը: Թվարկվածների մեծ մասը ուղղանկյան ձև ունի, հեռվից նայելիս նրանք նման են զուգահեռանիստի: Այդ պատճառով, հաճախ հարթությունը պատկերում են զուգահեռագծի տեսքով: Սակայն, հարթությունը կարելի է ներկայացնել նաև այլ կերպ:Հարթության օրինակներ բնության մեջ.
 սեղանի մակերևույթը |  սենյակի հատակը |
 գրքի մակերևույթը |  ջրի մակերևույթը |
Ինչպես հարթաչափության մեջ, երկու տարածաչափական մարմիններ կոչվում են հավասար, եթե նրանք համադրելիս համընկնում են:
Տարածաչափական մարմինների գլխավոր բնութագրիչը մարմնի ծավալն է:
Մարմնի ծավալը տարածության այն մասն է, որը սահմանափակում է այդ մարմինը:
Սահմանումից հետևում է, որ մարմնի ծավալի գաղափարը կախված չէ նրա դիրքից տարածության մեջ և այն հանգամանքից, թե ինչպիսի մասերից է այն բաղկացած:
Մարմնի ծավալի արժեքը հաշվում են հետևյալ երկու աքսիոմների վրա հիմնվելով՝
1) հավասար մարմիններն ունեն հավասար ծավալներ,
2) եթե մարմինը բաղկացած է չհատվող մասերից, ապա մարմնի ծավալը հավասար է նրա մասերի ծավալների գումարին:
Ծավալին թվային արժեք վերագրելու համար պետք է ընտրել ծավալի չափման միավորները:
Ծավալի չափման միավորը երկարության չափման մեկ միավոր կողով խորանարդի ծավալն է:
Եթե խորանարդի կողը \(1\) սմ է, ապա խորանարդի ծավալը հավասար է \(1\) սմ³, եթե խորանարդի կողը \(1\) մ է, ապա խորանարդի ծավալը հավասար է \(1\) մ³:
Հավասար ծավալներով մարմինները կոչվում են հավասարամեծ:
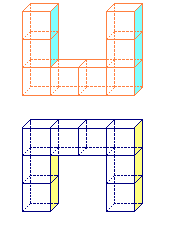 Հավասար մարմիններ | 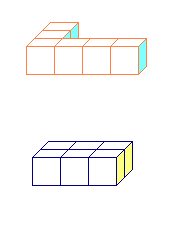 Հավասարամեծ մարմիններ |
Հավասար մարմինների ծավալը՝ \(8\) սմ³
Հավասարամեծ մարմինների ծավալը՝ \(6\) սմ³
Բոլոր հավասար մարմինները հավասարամեծ են, սակայն ոչ բոլոր հավասարամեծ մարմիններն են հավասար:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009