
















Տարածաչափության ներածություն
Հարթաչափությունը ուսումնասիրում է պատկերները հարթության մեջ և նրանց հատկությունները: Պատկերավոր ասած, հարթաչափությունը ուսումնասիրում է այն ամենն, ինչ կարելի է նկարել կամ գծել թղթի կտորի վրա:
Հարթաչափության հիմնական գաղափարներն են՝ կետը, ուղիղը և հարթ պատկերները (օրինակ՝ քառակուսի, եռանկյուն, շրջան, սեղան, շեղանկյուն և այլն):
Հարթաչափության ուսումնասիրած բոլոր կետերի բազմությունը կազմում է հարթություն:
Տարածաչափությունը ուսումնասիրում է պատկերները տարածության մեջ և նրանց հատկությունները: Պատկերավոր ասած, տարածաչափությունը ուսումնասիրում է այն ամենն, ինչ կարելի է սոսնձել թղթի կտորներից, պատրաստել տախտակներից և աղյուսներից և այլն:
Տարածաչափության հիմնական գաղափարներն են՝ կետը, ուղիղը, հարթությունը և տարածաչափական պատկերները (օրինակ՝ խորանարդ, բուրգ, ուղղանկյունանիստ, գլան, կոն, գունդ և այլն):
Տարածաչափության ուսումնասիրած բոլոր կետերի բազմությունը կոչվում է տարածություն:
Տարածաչափությունը նաև անվանում են հունարենից եկած ստերեոմետրիա բառով: Ստերեոմետրիա բառը առաջացել է հունարեն ստերեո՝ ծավալուն, տարածական և մետրեո՝ չափել բառերից:
Օրինակ
այս շարժական ներկայացումներում ցուցադրված են հարթաչափական և տարածաչափական պատկերների ընդհանրություններն ու տարբերությունները:
Քառակուսին հարթաչափության մեջ վերածվում է խորանարդի տարածաչափության մեջ:

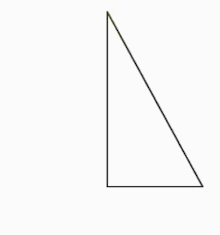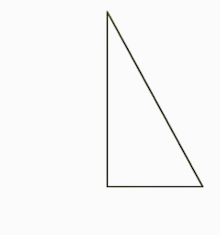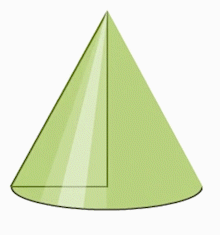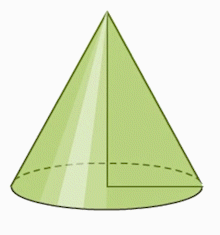
Ուղղանկյուն եռանկյունը էջերից մեկի շուրջը պտտելիս հարթաչափության մեջ վերածվում է կոնի՝ տարածաչափության մեջ:
Քանի որ ցանկացած ուղիղ և հարթություն բաղկացած են կետերից, ապա նրանք տարածաչափական պատկերներ են:
Հարթությունն անվերջ է, այն տարածությունը բաժանում է երկու մասի:
Կետերը նշանակում են լատիներեն մեծատառերով՝ \(A, B, C, D, E, K,…\)
Ուղիղները նշանակում են լատիներեն փոքրատառերով՝ \(a, b, c, d, e, k,…\)
Հարթությունները նշանակում են հունարեն տառերով՝ ,...
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009