
















Պատկերների համաչափությանը դուք արդեն ծանոթ եք: Մասնավորապես, արդեն դիտարկել ենք հարթ պատկերների կենտրոնային համաչափությունը:
Դրա օգնությամբ էլ սահմանվում է տարածական պատկերների կենտրոնային համաչափությունը:


Կենտրոնական համաչափություն
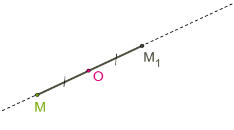
Տարածության \(M\) և կետերը կոչվում են\(O\) կետի նկատմամբ համաչափ, եթե \(O\) կետը հատվածի միջնակետն է՝ :
Այդ դեպքում ասում են, որ \(M\) և կետերը կենտրոնային համաչափ կետեր են, և \(O\) կետը համաչափության կենտրոնն է:
Դիտարկենք գնդի օրինակը:
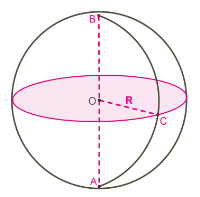
Դժվար չէ նկատել, որ եթե վերցնել գնդին պատկանող որևէ \(A\) կետ, ապա \(O\) կենտրոնի նկատմամբ նրան համաչափ \(B\) կետը ևս պատկանում է գնդին:
Սա հենց նշանակում է, որ գունդը կենտրոնային համաչափ տարածական մարմին է, և նրա կենտրոնը համաչափության կենտրոնն է:
Տարածական մարմինը կոչվում է \(O\) կետի նկատմամբ համաչափ, եթե նրա բոլոր կետերի՝ \(O\) կետի նկատմամբ համաչափ կետերը նույնպես այդ մարմնի կետեր են:
Այդ դեպքում ասում են, որ մարմինը օժտված է կենտրոնային համաչափությամբ:
\(O\) կետը կոչվում է մարմնի համաչափության կենտրոն:
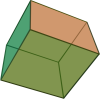
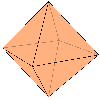
Կենտրոնային համաչափությամբ օժտված մարմինների օրինակներ են՝ խորանարդը, կանոնական ութանիստը, կանոնավոր վեցանկյուն պրիզման և այլն:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009