
















Արդեն դիտարկել ենք հարթ պատկերների առանցքային համաչափությունը:
Նման կերպով սահմանվում է տարածական պատկերների համաչափությունն ուղղի կամ հարթության նկատմամբ:


Առանցքային և հայելային համաչափություններ
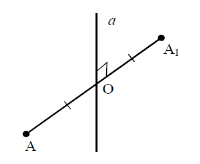
Տարածության \(A\) և կետերը կոչվում են \(a\) ուղղի նկատմամբ համաչափ, եթե \(a\) ուղիղը ուղղահայաց է հատվածին և անցնում է նրա \(O\) միջնակետով՝ :
Այդ դեպքում ասում են, որ \(A\) և կետերը առանցքային համաչափ կետեր են, և \(a\) ուղիղը համաչափության առանցքն է:
Նման ձևով սահմանվում է նաև համաչափությունը հարթության նկատմամբ:
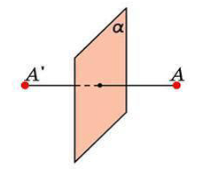
Տարածության \(A\) և կետերը կոչվում են հարթության նկատմամբ համաչափ, եթե հարթությունը ուղղահայաց է հատվածին և անցնում է նրա միջնակետով:
Այդ դեպքում ասում են, որ \(A\) և կետերը հայելային համաչափ կետեր են, և հարթությունը համաչափության հարթությունն է:
Այժմ կարող ենք սահմանել տարածական մարմնի առանցքային և հայելային համաչափությունները:
Տարածական մարմինը կոչվում է \(a\) ուղղի ( հարթության) նկատմամբ համաչափ, եթե նրա բոլոր կետերի՝ \(a\) ուղղի ( հարթության) նկատմամբ համաչափ կետերը նույնպես այդ մարմնի կետեր են:
Այդ դեպքում ասում են, որ մարմինն օժտված է առանցքային (հայելային) համաչափությամբ: \(a\) ուղիղը ( հարթությունը) կոչվում է համաչափության առանցք (հարթություն):
Դիտարկենք գլանի օրինակը:
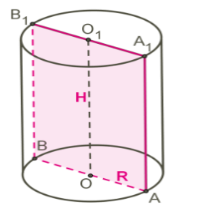
Դժվար չէ նկատել, որ -ը գլանի համար համաչափության առանցք է, իսկ -ը՝ համաչափության հարթություն:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009