
















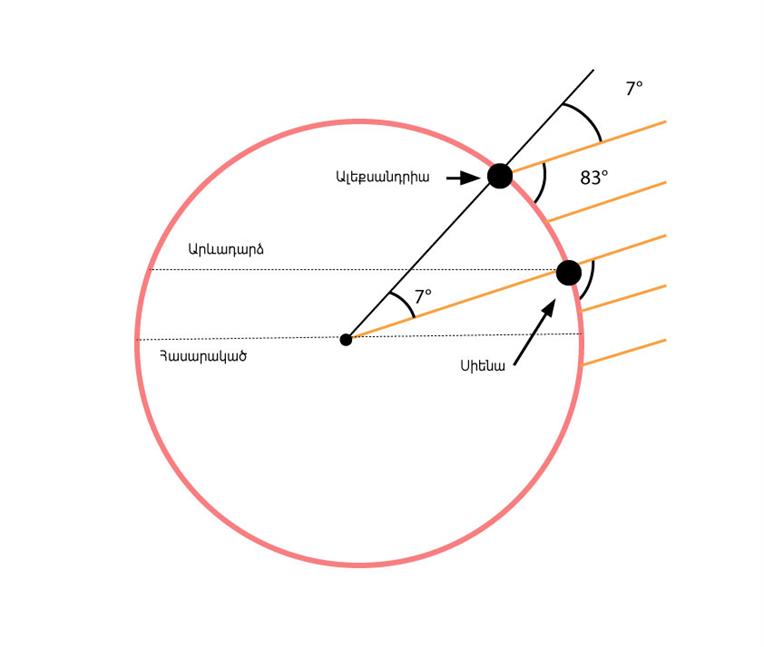
Երկրագնդի գնդաձևության մասին գիտեին դեռևս անտիկ աշխարհում: Էրատոսթենեսը գիտեր նաև, որ Սիեն քաղաքում ամառային արևակայության օրը (հունիսի \(22\)) Արեգակը կեսօրին լինում է ուղիղ զենիթում (ուղիղ գլխավերևում): Նույն պահին Սիենից հյուսիս գտնվող Ալեքսանդրիա քաղաքում Արեգակի ճառագայթների անկման անկյունը կեսօրին \(7\) աստիճանով պակաս ստացվեց (տես նկարը): Իմանալով այդ երկու քաղաքների միջև եղած հեռավորությունը՝ նա հաշվեց Երկրագնդի շրջագծի երկարությունը (շուրջ \(39600\) կմ, որը իրական չափից պակաս էր, ընդամենը մոտ \(400\) կմ է):
Եթե հայտնի է կետի աշխարհագրական լայնությունը, ապա կարելի է որոշել Արեգակի ճառագայթների անկման անկյունը բանաձևերի օգնությամբ:
Գիշերահավասարի օրերին (մարտի \(21\), սեպտեմբերի \(23\)) ճառագայթների անկման անկյունը Հայկական լեռնաշխարհի որևէ կետում կարելի է որոշել \(r = 90-a\) բանաձևով, որտեղ \(r\)-ը ճառագայթների անկման անկյունն է կեսօրին, իսկ \(a\)-ն՝ կետի աշխարհագրական լայնությունը:
Արևակայության օրերին (հունիսի \(22\), դեկտեմբերի \(22\)) ճառագայթների անկման անկյունը Հայկական լեռնաշխարհի որևէ կետում կարելի է որոշել \(r = 90-(a ± 23.5)\) բանաձևով:
Ինչպես գիտեք, քարտեզի մասշտաբը ցույց է տալիս, թե \(1\) սմ-ը քարտեզի վրա քանի սմ կամ կմ է իրականում (բնության մեջ): Հետևաբար մասշտաբի վերաբերյալ խնդիրները հանգում են երկու հիմնական ենթախնդրի.
\(1\) ենթախնդիր. տրված է քարտեզի մասշտաբը և կետերի միջև իրական \((1)\) կամ քարտեզային \((2)\) հեռավորությունը և պահանջվում է որոշել քարտեզային \((1)\) կամ իրական \((2)\) հեռավորությունը:
\(2\) ենթախնդիր. տրված է կետերի միջև իրական և քարտեզային հեռավորությունը, անհրաժեշտ է որոշել քարտեզի մասշտաբը:
Երկու դեպքում էլ պետք է հիշել, որ \(1\) կմ \(=\) \(100000\) սմ, հետևաբար առաջին ենթախնդրի դեպքում անհրաժեշտ է նախևառաջ մասշտաբը արտահայտել կիլոմետրերով: Դրա համար անհրաժեշտ է թվային մասշտաբի հայտարարի թիվը բաժանել \(100000\)-ի: Ինչից հետո, ելնելով տրված մյուս ցուցանիշից, գտնել քարտեզային \((2)\) կամ իրական \((1)\) հեռավորությունը:
Երկրորդ ենթախնդրի դեպքում, եթե պարզել ենք, թե քարտեզի վրա \(1\) սմ բնության մեջ քանի կմ է, թվային մասշտաբը ստանալու համար անհրաժեշտ է բնության մեջ երկու կետերի միջև հեռավորության արժեքը բազմապատկել \(100000\)-ով և գրել թվային մասշտաբի հայտարարում:
Մասշտաբի վերաբերյալ խնդիրներում երբեմն պահանջվում է որոշել ոչ թե օբյեկտի գծային երկարությունը, այլ զբաղեցրած տարածքը, ինչը նշանակում է, որ պետք է գտնել, թե քարտեզի վրա \(1\) սմ² մակերեսով տարածքը բնության մեջ որքան կմ² տարածք է զբաղեցնում և խնդիրը լուծել` ելնելով այդ ցուցանիշից նույն սկզբունքներով, ինչպես նախորդ ենթախնդիրներն էին:
Հայտնի է, որ Երկրի յուրաքանչյուր միջօրեականի երկարությունը մոտ \(20000\) կմ է, իսկ հասարակածի երկարությունը՝ մոտ \(40000\) կմ: Եթե երկրագնդի շրջագիծը և հասարակածը պատկերենք շրջանագծի տեսքով, կստանանք, որ դրանցից յուրաքանչյուրի \(1°\) աղեղի երկարությունը \(111\) կմ է, հետևաբար ցանկացած կետի հեռավորությունը հասարակածից, բևեռներից կամ նույն միջօրեականի վրա գտնվող մեկ այլ կետից հաշվելու համար անհրաժեշտ է դրանց լայնությունների տարբերությունը բազմապատկել \(111\) կմ-ով:
Աշխարհագրական ժամային գոտին ընդգրկում է \(15°\) լայնությամբ տարածք (\(360 : 24\) ժ \(= 15\) կամ \(± 7,5°\) ժամային գոտու կենտրոնով անցնող միջօրեականի նկատմամբ)։
Ժամային գոտիների հաջորդականության հաշվարկն արվում է զրոյական կամ Գրինվիչի միջօրեականից, որը զրոյական աշխարհագրական ժամային գոտու կենտրոնով անցնող միջօրեականն է: Երկրագունդ բաժանված է \(24\) ժամային գոտու:
Քանի որ զրոյական ժամային գոտին ավարտվում է ոչ թե զրոյական միջօրեականով, այլ նրանից \(7,5\) աստիճան արևելք և արևմուտք, ապա կամայական կետի աշխարհագրական ժամային գոտին որոշում ենք հետևյալ բանաձևով՝ \((A-7,5°)/15\), որտեղ \(A\)-ն տվյալ կետի աշխարհագրական երկայնությունն է, \(7,5°\)-ը` զրոյական միջօրեականի ավարտը, \(15\)-ը` մեկ ժամային գոտու լայնությունը: Եթե թիվը ստացվում է դիցուք \(7,1\), ապա դա նշանակում է, որ կետը գտնվում է \(8\)-րդ ժամային գոտում, այսինքն մնացորդի առկայության դեպքում կլորացումը միշտ կատարվում է դեպի հաջորդ ժամային գոտի:
«Հայաստանի Բնաշխարհ» հանրագիտարան, Երևան, 2006
Դպրոցական հանրագիտարան, Երևան 2009