Ռացիոնալ կողերով ուղղանկյունանիստի ծավալը

Մենք գիտենք, թե ինչպես հաշվել ուղղանկյունանիստի (կամ խորանարդի) ծավալը, եթե նրա կողերի երկարությունները բնական թվեր են`

V = a \cdot b \cdot c

, որտեղ

a, b, c

բնական թվերը ուղղանկյունանիստի կողերի երկարություններն են:

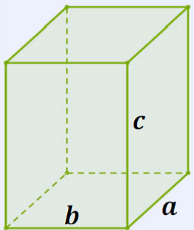
Իսկ ինչպե՞ս հաշվել ծավալը, եթե կողերի երկարությունները կոտորակային թվեր են:

Օրինակ

Դիտարկենք այս խորանարդը, որի բոլոր կողերի երկարությունները \(1\) սմ են:

Մեծ խորանարդը բաժանված է \(3\) շերտի: Յուրաքանչյուր շերտում կա \(9\) փոքր խորանարդիկ: Արդյունքում, մեծ խորանարդը բաժանված է \(27 = 3·9\) հավասար փոքր խորանարդիկների:

Փոքր խորանարդիկի կողը \(3\) անգամ փոքր է մեծ խորանարդի կողից, և քանի որ մեծ խորանարդի կողի երկարությունը \(1\) սմ է, ապա փոքր խորանարդիկի կողի երկարությունը կլինի

\frac{1}{3}

սմ:

Հաշվենք մեծ խորանարդի ծավալը:

Քանի որ

a = b = c = 1

սմ, ապա

V_{մեծ} = a \cdot b \cdot c = 1 \cdot 1 \cdot 1 = 1

սմ²

Քանի որ մեծ խորանարդը բաղկացած է \(27\) իրար հավասար փոքր խորանարդիկներից, ապա յուրաքանչյուր խորանարդիկի ծավալը հավասար կլինի

V_{փոքր} = \frac{V_{մեծ}}{27} = \frac{1}{27}

սմ²:

Նկատում ենք, որ

V_{փոքր} = \frac{1}{27} = \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3}

սմ², և քանի որ փոքր խորանարդիկի բոլոր կողերը

\frac{1}{3}

սմ են, ապա համոզվում ենք, որ

V = a \cdot b \cdot c

բանաձևը ճիշտ է նաև այս դեպքում:

Նույն եզրակացությանն ենք գալիս նաև հետևյալ դեպքում:

Օրինակ

Նորից դիտարկենք նույն

a = b = c = 1

սմ կողերով խորանարդը, որն այս անգամ բաժանված է \(36 = 12·3\) փոքր մասերի: Այս դեպքում դրանք փոքր զուգահեռանիստեր են:

Փոքր զուգահեռանիստերի կողերը հավասար են՝

\frac{1}{3}

սմ,

\frac{1}{3}

սմ և

\frac{1}{4}

սմ:

Արդեն գիտենք, որ մեծ խորանարդի ծավալը

V_{մեծ} = a \cdot b \cdot c = 1 \cdot 1 \cdot 1 = 1

սմ² է:

Քանի որ այս անգամ մեծ խորանարդը բաժանված է \(36\) հավասար զուգահեռանիստների, ապա

V_{փոքր} = \frac{V_{մեծ}}{36} = \frac{1}{36}

սմ²

Նկատում ենք, որ

V_{փոքր} = \frac{1}{36} = \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{4}

, և նորից

V = a \cdot b \cdot c

բանաձևը ճիշտ է:

Ուղղանկյունանիստի ծավալի հաշվման բանաձևերը

Այսպիսով, իմանալով զուգահեռանիստի երեք կողերը՝ չափումները, կարողանում ենք հաշվել ուղղանկյունանիստի ծավալը:

V = a \cdot b \cdot c

բանաձևը ճիշտ է ցանկացած

a, b, c

ռացիոնալ կողերով զուգահեռանիստի դեպքում:

Նկատի ունենալով, որ

a \cdot b

-ն ուղղանկյունանիստի հիմքի մակերեսն է (նայիր առաջին նկարին), իսկ

c

-ն՝ բարձրությունը, ապա

Ուղղանկյունանիստի ծավալը հավասար է նրա հիմքի մակերեսի և բարձրության արտադրյալին՝

V = S_{հիմք} \cdot c

Ծավալի չափման միավորները

Ծավալի չափման միավորներն են՝

{մմ}^{3}, {սմ}^{3}, {դմ}^{3}, մ^{3}, {կմ}^{3}

\begin{array}{l} 1 {կմ}^{3} = 1000 000 000 մ^{3} \\ 1 մ^{3} = 1000 {դմ}^{3} = 1000 000 {սմ}^{3} \\ 1 {դմ}^{3} = 1000 {սմ}^{3} \\ 1 {սմ}^{3} = 1000 {մմ}^{3} \end{array}

Աղբյուրները

Բ. Նահապետյան, Ա. Աբրահամյան, Մաթեմատիկա 6-րդ դասարան, ՄԱՆՄԱՐ, 2012:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Ռացիոնալ կողերով ուղղանկյունանիստի ծավալը

Տեսություն