Ուղղանկյունանիստի լրիվ մակերևույթի մակերեսը

Մեզ արդեն ծանոթ է այնպիսի երկրաչափական պատկեր, ինչպիսին է ուղղանկյունանիստը:

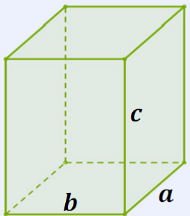
Ուղղանկյունանիստի մակերևույթը բաղկացած է \(6\) ուղղանկյունաձև նիստերից՝ \(4\) կողմնային նիստերից և \(2\) հիմքերից:

Հանդիպակաց նիստերն իրար հավասար են, հետևաբար հավասար են նաև նրանց մակերեսները:

Ուղղանկյունանիստի լրիվ մակերևույթի մակերեսը հավասար է նրա բոլոր նիստերի մակերեսների գումարին:

Ուստի, այն հաշվվում է հետևյալ բանաձևով՝

S_{լրիվ} = S_{կողմն} {+ 2 \cdot S}_{հիմք}

Վերևի նկարից երևում է, որ (հանդիպակաց նիստերը հավասար են)

S_{կողմն} = 2 ac + 2 bc

S_{հիմք} = ab

Գումարելով այս բանաձևերը (հաշվի առնելով, որ ուղղանկյունանիստն ունի \(2\) հիմք), ստանում ենք ուղղանկյունանիստի լրիվ մակերևույթի մակերեսի բանաձևը՝

S_{լրիվ} = 2 \cdot (ab + ac + bc)

, որտեղ

a

-ն,

b

-ն և

c

-ն ուղղանկյունանիստի չափումներն են:

Այս բանաձևը ճիշտ է ցանկացած ուղղանկյունանիստի համար, որի

a

b

c

չափումները դրական ռացիոնալ թվեր են:

Ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

Խորանարդի նիստերը իրար հավասար \(6\) քառակուսիներ են \((\)

a = b = c

\()\)

Խորանարդի դեպքում լրիվ մակերևույթի մակերեսի բանաձևը էապես պարզ տեսք ունի:

Փորձիր ինքնուրույն դուրս բերել այդ բանաձևը:

Աղբյուրները

Բ. Նահապետյան, Ա. Աբրահամյան, Մաթեմատիկա 6-րդ դասարան, ՄԱՆՄԱՐ, 2012:

Սխա՞լ ես գտել

1. Ուղղանկյունանիստի լրիվ մակերևույթի մակերեսը