1. Ռացիոնալ թվերի պատկերումը կոորդինատային հարթության վրա

Մենք արդեն ծանոթ ենք կոորդինատային հարթության գաղափարին: Գիտենք, որ ամբողջ կոորդինատներով ցանկացած կետ պատկերվում է այդ հարթության վրա:

 

Օրինակ՝ ներքևի նկարում $G\left(1;0\right),H\left(0;-1\right),F\left(-1;0\right)$ կետերը գտնվում են կոորդինատային առանցքների վրա և ունեն ամբողջ կոորդինատներ:

 

Ամբողջ կոորդինատներ ունեն նաև $K\left(2;2\right),P\left(-1;1\right)$ կետերը:

 

$K$ կետի աբսցիսը հավասար է $4$ վանդակի ($O\left(0;0\right)$ սկզբնակետից դեպի աջ), իսկ օրդինատը՝ $4$ վանդակի (դեպի վերև):

 

Նույն ձևով տեսնում ենք, որ $P$ կետի աբսցիսը հավասար է $2$ վանդակի (դեպի ձախ), իսկ օրդինատը՝ $2$ վանդակի (դեպի վերև):

 

 

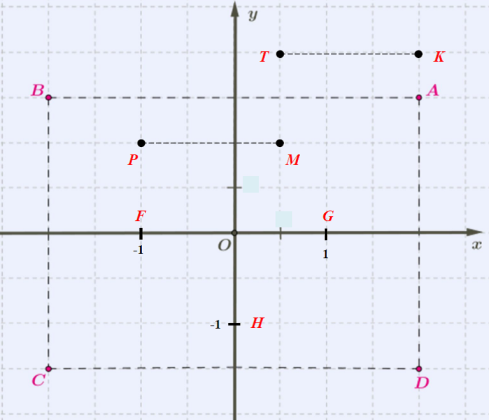
Իսկ ի՞նչ կոորդինատներ ունի, օրինակ՝ $M$ կետը:

 

Նկատում ենք, որ $M$ կետի աբսցիսը հավասար է $1$ վանդակի (դեպի աջ), իսկ օրդինատը՝ $2$ վանդակի (դեպի վերև):

 

Այսպիսով $M$ կետի կոորդինատներն են՝ $M\left(\frac{1}{2};1\right)$

Տեսնում ենք, որ կոորդինատային հարթության վրա կան կետեր, որոնց կոորդինատները կոտորակային թվեր են:

Նույն ձևով գտնում ենք մյուս կետերի կոորդինատները՝

 

 

Տեսնում ենք, որ կոորդինատային հարթության կետերի կոորդինատները կարող են լինել ոչ միայն ամբողջ թվեր, այլ նաև դրական կամ բացասական կոտորակներ և խառը թվեր:

 

Հիշենք, որ այդ թվերի համախմբությունը կազմում է ռացիոնալ թվերի բազմությունը: