1. Մեծությունների չափումը

Մենք արդեն գիտենք, թե ինչպես են չափում երկարությունները, մակերեսները, զանգվածները, արագությունները: Հիշենք, օրինակ, թե ինչպես են չափում հատվածի երկարությունը:

 

Առաջին հերթին պետք է ունենալ չափման միավորն ու գործիքը:

 

 

Վերցնենք $1$ սմ բաժանումներով քանոն և նրա միջոցով փորձենք չափել $\mathit{AB}$ հատվածի երկարությունը:

 

 

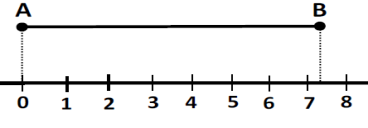
Տեսնում ենք, որ $\mathit{AB}$ հատվածի երկարությունը մեծ է $7$ սմ-ից և փոքր է $8$ սմ-ից:

 

Եթե համարենք, որ

 

1. $\left|\mathit{AB}\right|=7$ սմ, ապա մենք հաշված կլինենք հատվածի երկարության մոտավոր արժեքը պակասորդով:

 

2. $\left|\mathit{AB}\right|=8$ սմ, ապա մենք հաշված կլինենք հատվածի երկարության մոտավոր արժեքը հավելուրդով:

 

Այս դեպքում ասում են, որ $7$ սմ-ը և $8$ սմ-ը հատվածի մոտավոր արժեքներն են $1$ սմ-ի ճշգրտությամբ:

 

Ինչպե՞ս կարելի է մեծացնել չափումների ճշգրտությունը:

 

 

 

Օրինակ՝ եթե $\mathit{AB}$ հատվածի երկարությունը չափեինք միլիմետրերով, ապա կստանայինք հատվածի երկարության ճշգրիտ արժեքը՝ $73$ մմ:

Օրինակ՝ եթե համարում ենք, որ $\left|\mathit{AB}\right|=7$ սմ, ապա մեր չափման սխալանքը կլինի՝ $73-70=3$ մմ:

 

Իսկ եթե համարել, որ $\left|\mathit{AB}\right|=8$ սմ, ապա սխալանքը կլինի՝ $80-73=7$ մմ:

 

Տեսնում ենք, որ առաջին չափումն ավելի ճշգրիտ է:

 

Դիտարկենք երկարության չափման մեկ այլ օրինակ:

Մոտավոր հաշվարկի դեպքում օգտագործում են հետևյալ գրելաձևը՝ $7980\approx 8000$