
















Համաչափության հատկություն
Նայիր այս պատկերներին:

Պատկերները միանգամայն տարբեր են իրարից, և հնարավոր չէ դրանք շփոթել միմյանց հետ: Սակայն նրանք բոլորն ունեն մի կարևոր հատկություն. այս պատկերները համաչափ են:
Լավ պատկերացնելու համար համաչափության հատկությունը, նայիր այս պատկերներին, որոնք համաչափ չեն:
Պատկերի համաչափությունը նշանակում է, որ գոյություն ունի մի ուղիղ (այն կոչվում է պատկերի համաչափության առանցք), որը պատկերը բաժանում է միանման տեսք ունեցող երկու մասերևի՝ ձախ և աջ: Դրանք միանման են այն առումով, որ եթե ուղղի երկայնքով ծալել թուղթը, որի վրա նկարված է պատկերը, ապա ձախ և աջ մասերը կհամընկնեն:
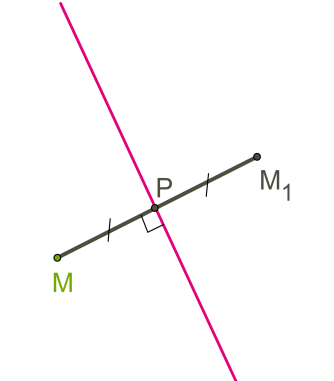
Ասում են, որ \(\)\(\) և \(\)\(\) կետերը համաչափ են \(\)\(\) ուղղի նկատմամբ,եթե այդ ուղիղը ուղղահայաց է \(\)\(\) հատվածին և անցնում է նրա միջնակետով:
Տրված ուղղի նկատմամբ և համաչափ կետերը կառուցելու համար պետք է՝
1) տանել ուղղի ուղղահայաց որևէ ուղիղ,
2) այդ ուղղի վրա նշել երկու կետեր, որոնք ունեն ուղղից միևնույն հեռավորությունը և գտնվում են նրա տարբեր կողմերում:
Երկու պատկերներ կոչվում են որևէ ուղղի նկատմամբ համաչափ, եթե նրանցից յուրաքանչյուրը կազմված է մյուսի կետերին համաչափ կետերից:
Ասում են, որ պատկերը օժտված է առանցքային համաչափությամբ, եթե գոյություն ունի այնպիսի ուղիղ, որը պատկերը բաժանում է այդ ուղղի նկատմամբ երկու համաչափ մասերի:
Համաչափ պատկերները հաճախ հանդիպում են իրական կյանքում՝

և բնության մեջ՝

Աղբյուրները
Բ. Նահապետյան, Ա. Աբրահամյան, Մաթեմատիկա 6-րդ դասարան, ՄԱՆՄԱՐ, 2012