1. Կոտորակների հիմնական հատկությունը, կրճատում

Դիտարկենք այս երեք նկարները, որոնցում կանաչով ներկված է շրջանի կեսը:

 

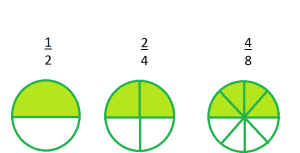
Առաջին նկարում ներկված է շրջանի $\frac{1}{2}$-ը, երկրորդում՝ $\frac{2}{4}$-ը և երրորդում՝ $\frac{4}{8}$-ը:

Բոլոր երեք կոտորակները իրար հավասար են՝ $\frac{1}{2}=\frac{2}{4}=\frac{4}{8}$, բայց դրանց համարիչներն ու հայտարարները տարբեր են: 

 

Նկատենք, որ առաջին կոտորակի համարիչն ու հայտարարը \(2\) անգամ փոքր են երկրորդի համարիչից և հայտարարից, իսկ երրորդ կոտորակի համարիչն ու հայտարարը \(4\) անգամ մեծ են առաջինի համարիչից և հայտարարից:

 

Այսինքն՝ $\frac{1}{2}=\frac{2:2}{4:2}=\frac{4:4}{8:4}$ կամ $\frac{4}{8}=\frac{2\cdot 2}{4\cdot 2}=\frac{1\cdot 4}{2\cdot 4}$