
















Սկզբնական տեղեկություններ կետերի, ուղիղների, ճառագայթների և հատվածների մասին
Երկրաչափությունը ամենահին գիտություններից մեկն է: Այն ուսումնասիրում է պատկերները, նրանց հատկությունները և փոխադարձ դիրքը:
Առաջին երկրաչափական փաստերը գտնված են բաբելոնյան սեպագիր աղյուսակներում (մ.թ.ա. \(III\)-րդ հազարամյակ) և այլ աղբյուրներում: Շատ պատկերների անվանումներ գալիս են հունարեն և լատիներեն (հին Հռոմի լեզուն) լեզուներից:
Պատկերներ կազմելու համար կօգտագործենք կետեր և ուղիղներ: Այս պատկերների միջոցով մենք կկազմենք մնացած բոլոր երկրաչափական պատկերները, իսկ կետը և ուղիղը կփորձենք պատկերացնել: Կետը՝ որպես անվերջ փոքր մի բան, իսկ ուղիղը՝ որպես երկու կողմի վրա անվերջ շարունակվող մի բան:
Կետերը նշանակում են լատիներեն մեծատառերով, իսկ ուղիղները՝ լատիներեն մեկ փոքրատառով կամ երկու լատիներեն մեծատառերով: Կետի և ուղղի փոխադարձ դիրքը բառերով կարելի է նկարագրել այսպես՝
- կետը գտնվում է (ընկած է) ուղղի վրա, կամ ուղիղը անցնում է (տարված է) կետով,
- կետը չի գտնվում (ընկած չէ) ուղղի վրա, կամ ուղիղը չի անցնում (տարված չէ) կետով:
Ուղղի այն մասը, որը սահմանափակված է երկու կետերով, կոչվում է հատված:
Կետը և նրանով սահմանափակված ուղղի մասը, կոչվում է ճառագայթ:
Հատվածի սահմանման համար տառերի հերթականությունը դեր չի խաղում՝ \(AB\) և \(BA\) հատվածները համընկնում են:
Ճառագայթի նշանակման մեջ առաջին տառը նրա սկզբնակետն է:
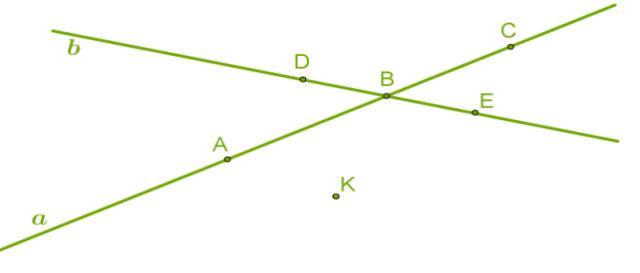
Օրինակ
Գծագրի նկարագիրը:
- Գծված են \(a\) և \(b\) ուղիղները: Դրանք կարելի է նշանակել նաև \(AC\) և \(DE\):
- Տրված ուղիղները հատվում են \(B\) կետում:
- \(K\) կետը չի գտնվում ուղիղներից ոչ մեկի վրա, այսինքն՝ ուղիղները չեն անցնում այդ կետով:
- \(AC\), \(AB\) և \(BC\) հատվածները գտնվում են \(a\) ուղղի վրա, \(AB\) և \(BC\) հատվածները ունեն ընդհանուր ծայրակետ՝ \(B\) կետը:
- \(BA\) և \(BC\) հակուղղված ճառագայթները գտնվում են \(a\) ուղղի վրա, իսկ \(BD\) և \(BE\) ճառագայթները՝ \(b\) ուղղի վրա:
 | Ուղիղների, ճառագայթների և հատվածների հատկությունները 1. Երկու կետերով կարելի է տանել միայն մեկ ուղիղ: 2. Երկու ուղիղներ կարող են հատվել միայն մեկ կետում: 3. Հատվածները հավասար են, եթե հավասար են դրանց երկարությունները: |
Աղբյուրները
նկարը http://www.myshared.ru կայքից
Բ. Նահապետյան, Ա. Աբրահամյան, Մաթեմատիկա 5-րդ դասարան, Մակմիլան-Արմենիա, 2006: