
















Նկարում ցուցադրված է \(2\) սմ, \(3\) սմ և \(5\) սմ կողերով ուղղանկյունանիստ:
Հաշվենք դրա ծավալը:
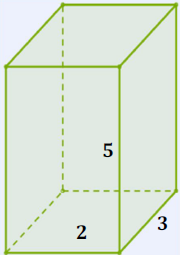
Ուղղանկյունանիստի ծավալը հավասար է հիմքի մակերեսի և բարձրության արտադրյալին:
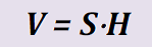
Հիմքի մակերեսը՝ \(S = 3 · 2\) սմ²,
բարձրությունը՝ \(H = 5\) սմ:
Ծավալը կլինի՝
\(V = (3 · 2) · 5\) սմ³
\(V = 6 · 5 = 30\) սմ³
Շրջենք նույն ուղղանկյունանիստը և նորից հաշվենք դրա ծավալը:
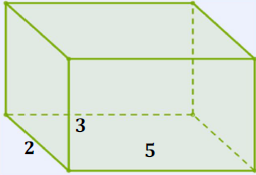
Այս անգամ կունենաք՝
հիմքի մակերեսը՝ \(S = 2 · 5\) սմ² է,
բարձրությունը՝ \(H = 3\) սմ:
Ծավալը կլինի՝
\(V = (2 · 5) · 3\) սմ³
Օգտվելով բազմապատկման տեղափոխական հատկությունից, կարելի է արտադրիչների տեղերը փոխել՝
\(V = 3 · (2 · 5)\) սմ³
\(V = 3 · 10 = 30\) սմ³
Այսպիսով, նույն ուղղանկյունանիստի համար (ուղիղ և շրջած) ստացանք ծավալի երկու արտահայտություններ՝
\(V = (3 · 2) · 5\) սմ³ և \(V = 3 · (2 · 5)\) սմ³
Տեսանք, որ երկու ձևերով ծավալը հաշվելիս ստացվում է նույն արժեքը՝ \(V = 30\) սմ³:
Եզրակացություն՝ \((3 · 2) · 5\)\(=\)\(3 · (2 · 5)\):
Այս կանոնը ճիշտ է նաև ընդհանուր դեպքում:
Երկու թվերի արտադրյալը երրորդ թվով բազմապատկելիս կարելի է առաջին թիվը բազմապատկել երկրորդ և երրորդ թվերի արտադրյալով:
Այս կանոնը կոչվում է բազմապատկման զուգորդական հատկություն:
Օրինակ
Աղբյուրները
Ս. Մկրտչյան, Ս. Իսկանդարյան, Ա. Աբրահամյան, Ռ. Սարգսյան, Մաթեմատիկա 4-րդ դասարան, Զանգակ, 2013