
















Մնացորդով բաժանում 10-ի, 100-ի, 1000-ի
Ուշադիր նայիր այս բաժանումներին:
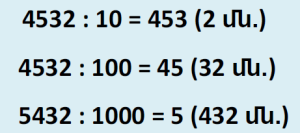
Բոլոր երեք բաժանումներում նկատվում է հետևյալ օրինաչափությունը՝ եթե հավասարությունների աջ մասերում անտեսել փակագծերի նշանները և «մն.» գրառումը, ապա կստացվի բաժանելին:
Հետևաբար, \(10\)-ի, \(100\)-ի և \(1000\)-ի բաժանելիս հաշվարկներ կատարել պետք չի, պետք է պարզապես ճիշտ տեղադրել մնացորդը ցույց տվող փակագծերը:
Եթե բաժանելիի թվանշանների մեջ զրոներ չկան, ապա՝
\(10\)-ի բաժանելիս մնացորդում մնում է բաժանելիի վերջին թվանշանը,
\(100\)-ի բաժանելիս մնացորդում մնում են բաժանելիի վերջին երկու թվանշանները,
\(1000\)-ի բաժանելիս մնացորդում մնում են բաժանելիի վերջին երեք թվանշանները:
\(10\)-ի, \(100\)-ի և \(1000\)-ի բաժանման քանորդը որոշվում է հետևյալ կանոնի միջոցով:
Թիվը \(10\)-ի բաժանելիս քանորդում ստացվում է այդ թվի տասնյակների քանակը:
Թիվը \(100\)-ի բաժանելիս քանորդում ստացվում է այդ թվի հարյուրյակների քանակը:
Թիվը \(1000\)-ի բաժանելիս քանորդում ստացվում է այդ թվի հազարյակների քանակը:
Դիտարկված դեպքերում բաժանումը կատարվեց մնացորդով:
Հետագայում մենք կպարզենք, թե ե՞րբ է թիվը անմնացորդ բաժանվում \(10\)-ի, \(100\)-ի և \(1000\)-ի: Այս պահին ընդամենը նշենք, որ մնացորդը առաջացավ այն պատճառով, որ բաժանելիի թվանշանները զրոյից տարբեր են:
Օրինակ
Կատարենք տրված բաժանումները:
1. \(630 : 10 = 63\)
2. \(905 : 10 = 90 (5 մն.)\)
3. \(560 : 100 = 5 (60 մն.)\)
4. \(8701 : 1000 = 8 (701 մն.)\)
Աղբյուրները
Ս. Մկրտչյան, Ս. Իսկանդարյան, Ա. Աբրահամյան, Ռ. Սարգսյան, Մաթեմատիկա 4-րդ դասարան, Զանգակ, 2013