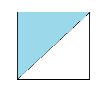
Քառակուսին բաժանված է երկու հավասար մասերի, ներկված է -րդ մասը: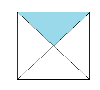
Քառակուսին բաժանված է չորս հավասար մասերի, ներկված է -րդ մասը:
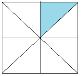Քառակուսին բաժանված է ութ հավասար մասերի, ներկված է -րդ մասը:Տեսնում ենք, որ ամենամեծը առաջին կապույտ եռանկյունն է, իսկ ամենափոքրը՝ վերջինը:
Ուշադրություն
Որքան շատ են մասերը, այնքան փոքր է դրանցից յուրաքանչյուրը:
Ներքևի նկարներում միևնույն չափի պիցան բաժանված է \(6\), \(8\) և \(10\) հավասար մասերի:
\(6\) մասի \(8\) մասի \(10\) մասի
\(6\) մասի բաժանված պիցայի յուրաքանչյուր մասը հավասար է ամբողջ պիցայի -ին:
\(8\) մասի բաժանված պիցայի յուրաքանչյուր մասը հավասար է ամբողջ պիցայի -ին:
\(10\) մասի բաժանված պիցայի յուրաքանչյուր մասը հավասար է ամբողջ պիցայի -ին:
Երեք նկարներում պիցան հաջորդաբար բաժանվում է ավելի շատ մասերի՝ \(6 < 8 < 10\):
Տեսնում ենք, որ մասերը շատանալիս պիցայի մեկ բաժինը փոքրանում է:
Հետևաբար,
\(>\) \(>\)
Նկատած օրինաչափությունը ընդհանուր կանոն է:
Որքան շատ մասերի ենք բաժանում թիվը, այնքան մասը փոքրանում է:
Աղբյուրները
Ս. Մկրտչյան, Ս. Իսկանդարյան, Ա. Աբրահամյան, Ռ. Սարգսյան, Մաթեմատիկա 4-րդ դասարան, Զանգակ, 2013: