
















Հավասար պատկերներ
Եթե պատկերները վերադրելիս համընկնում են, ապա այդպիսի պատկերներն անվանում են հավասար պատկերներ:
Հետևյալ նկարում ցուցադրված են հինգ համարակալված ուղղանկյուններ:
Որո՞նք են դրանցից իրար հավասար:

\(1\)-ը հավասար չէ \(2\)-ին, քանի որ \(1\)-ի բոլոր կողմերը հավասար են, իսկ \(2\)-ինը՝ ոչ:
\(1\)-ը հավասար չէ \(3\)-ին, քանի որ \(1\)-ի կողմերը փոքր են \(3\)-ի կողմերից:
Դրանք վերադրելիս չեն համընկնի:
Հավասար պատկերներն են՝ \(1\)-ը և \(4\)-ը, \(2\)-ը և \(5\)-ը:
Հետևյալ նկարում ցուցադրված չորս եռանկյուններից որո՞նք են իրար հավասար:
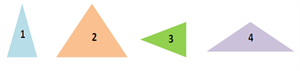
\(1\)-ը և \(4\)-ը հավասար չեն \(2\)-ին, քանի որ \(2\)-ի բոլոր կողմերը հավասար են, իսկ \(1\)-ի և \(4\)-ի կողմերը՝ ոչ:
\(1\)-ը հավասար չէ \(4\)-ին, քանի որ \(1\)-ի վերևի անկյունը սուր է, իսկ \(4\)-ինը՝ բութ:
Դրանք վերադրելիս չեն համընկնի:
Հավասար պատկերներն են՝ \(1\)-ը և \(3\)-ը:
Հետևյալ նկարում ցուցադրված չորս պատկերներից որո՞նք են իրար հավասար:
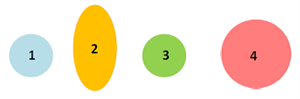
\(1\)-ը հավասար չէ \(2\)-ին, քանի որ \(1\)-ը շրջան է, իսկ \(2\)-ը՝ ոչ:
\(1\)-ը հավասար չէ \(4\)-ին, քանի որ \(1\)-ի շառավիղն ավելի փոքր է:
Դրանք վերադրելիս չեն համընկնի:
Հավասար պատկերներն են՝ \(1\)-ը և \(3\)-ը:
Աղբյուրները
Ս. Մկրտչյան, Ս. Իսկանդարյան, Ա. Աբրահամյան, Մաթեմատիկա 3-րդ դասարան, Զանգակ, 2014: