Պատկերի մակերեսը, ուղղանկյան մակերեսը, մակերեսների համեմատում
Պատկերների մակերեսները համեմատելու համար կարելի է դրանք վերադրել:
Օրինակ, վերադրելիս այս շրջանն ամբողջությամբ տեղավորվեց քառակուսու ներսում:
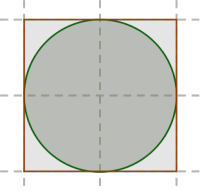
Հետևաբար, շրջանի մակերեսը փոքր է քառակուսու մակերեսից:
Համեմատենք հետևյալ պատկերների մակերեսները:

Այս պատկերների մակերեսները համեմատելու համար կարելի է հաշվել, թե քանի՞ փոքրիկ քառակուսիներից է կազմված պատկերներից յուրաքանչյուրը և համեմատել ստացված թվերը:
Առաջին պատկերը կազմված է \(6\) քառակուսիներից, իսկ երկրորդ պատկերը կազմված է \(9\) քառակուսիներից:
Հետևաբար, առաջին պատկերի մակերեսը փոքր է երկրորդ պատկերի մակերեսից:
Ինչպե՞ս հաշվել ուղղանկյան մակերեսը:
Կանոնն այսպիսին է.
Ուղղանկյան մակերեսը հավասար է լայնության և երկարության արտադրյալին:
Հաշվենք, օրինակ, այս ուղղանկյան մակերեսը (ցանցի քառակուսիներից յուրաքանչյուրի կողմը \(1\) սմ է):

Ուղղանկյունը կազմված է \(8\) քառակուսիներից, որոնցից յուրաքանչյուրի մակերեսը \(1\) սմ² է, հետևաբար, ուղղանկյան մակերեսը \(8\) սմ² է:
Նույն թիվը ստանում ենք նաև ըստ կանոնի: Իրոք, քանի որ ուղղանկյան կողմերի երկարությունները \(2\) սմ և \(4\) սմ են, ապա, ըստ կանոնի, մակերեսը կլինի՝ \(2 · 4 = 8\) սմ²:
Աղբյուրները
Ս. Մկրտչյան, Ս. Իսկանդարյան, Ա. Աբրահամյան, Մաթեմատիկա 3-րդ դասարան, Զանգակ, 2014: