Համակարգչում թվային ինֆորմացիայի կոդավորումն ուսումնասիրելու համար նախ եկեք տեսնենք, թե տասական թիվը իրականում ինչպե՞ս է ձևավորվում:
\( \)
Օրինակ
\(345\) թիվն ուսումնասիրելիս նկատում ենք, որ այն պարունակում է \(3\) հարյուրակ, \(4\) տասնյակ և \(5\) միավոր: Այսպիսով ստացվում է, որ
Չնայած բերված օրինակը վերաբերում է տասական համակարգին` պետք է ասել, որ երկուական համակարգի թիվը տասական համակարգում ներկայացնելու համար նորից պետք է ելնել վերը նշված օրինաչափությունից: Օրինակ` երկուական \(101101\)թիվը տասական համակարգում ներկայացնելու համար անհրաժեշտ է կազմակերպել գումար, որտեղ յուրաքանչյուր գումարելի ստացվում է թվի համապատասխան թվանշանը բազմապատկելով երկուսի այն աստիճանով, որ դիրքում գտնվում է այդ թվանշանը: Թվի մեջ թվանշանների դիրքերի համարակալումը կատարվում է աջից ձախ, սկսած նախնական \(0\)-ից:
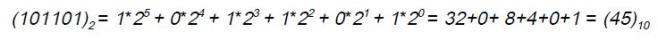
Տասական թիվը երկուական համակարգում ներկայացնելու համար անհրաժեշտ է հաջորդաբար իրականացնել հետևյալ գործողությունները`
* թիվը բաժանել \(2\)-ի,
* առանձնացնել բաժանման արդյունքում ստացված ամբողջ մնացորդը, իսկ քանորդը նորից բաժանել \(2\)-ի,
* բաժանումների և մնացորդների առանձնացման գործընթացը կրկնել այնքան, քանի դեռ ստացվող քանորդը մեծ է կամ հավասար \(2\)-ի,
* թվի երկուական ներկայացումը ստանալ` հաջորդաբար վերջից մինչև սկիզբ առանձնացված մնացորդների կցագրմամբ:
Օրինակ` տասական \(97\)ամբողջ թիվը ներկայացնենք երկուական համակարգում.
Առանձնացված մնացորդների` վերջից դեպի սկիզբ հաջորդական կցագրմամբ կստանանք տասական \(97\) թվի երկուական գրառումը`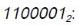 
Աղյուսակում բերված են \(0\)-ից \(15\) տասական ամբողջ թվերի երկուական համարժեքները՝
Եթե ստեղնաշարի յուրաքանչյուր տառա-թվային ստեղնի համապատասխանության մեջ դնենք որոշակի ամբողջ թիվ (օրինակ` համար), ապա վերջինիս երկհիմնային կոդի օգնությամբ, այսպիսով, կարելի է կոդավորել նաև տեքստային ինֆորմացիան:
Համակարգչում յուրաքանչյուր պայմանանշանի կոդավորման համար հատկացվում է մեկ բայթ ծավալով հիշողություն, այսինքն` ութ բիթ: Քանի որ յուրաքանչյուր բիթ կարող է ընդունել ընդամենը երկու հնարավոր արժեքներ`\(0\) կամ 1, ապա \(8\) բիթի օգնությամբ կարելի է կոդավորել
տարբեր պայմանանշաններ, որոնք համարակալվում են \(0\)-ից մինչև \(255\) ամբողջ թվերով: Այսքանը բավարարում է կոդավորելու լատինական, ռուսական և հայկական այբուբենի մեծատառերն ու փոքրատառերը, \(0\)-ից \(9\) թվանշանները, կետադրության նշանները, թվաբանական գործողությունների հիմնական պայմանանշանները և որոշ քանակությամբ հատուկ այլ պայմանանշաններ:Մյուս աղյուսակում ներկայացված են որոշ պայմանանշանների կոդեր: Բերված աղյուսակի օգնությամբ, օրինակ, կոդ բառը կարելի է ներկայացնել \(11001111 11100001 10111001\) երկուական թվի տեսքով:
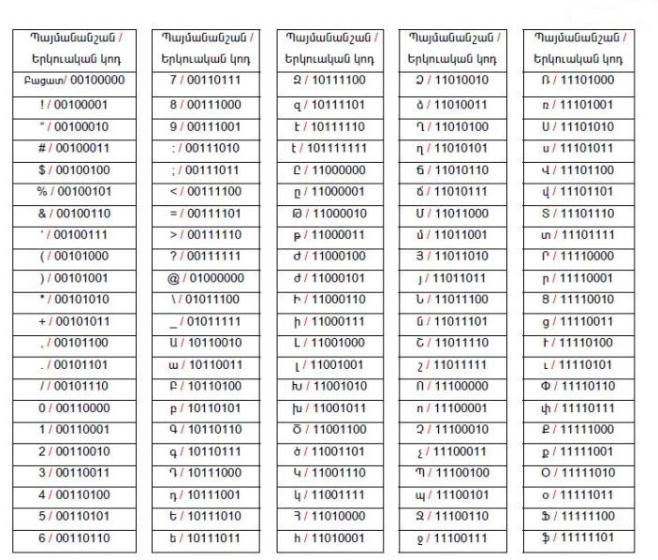
Եթե երկուական կոդը ութից պակաս թվանշաններ է պարունակում, ապա անհրաժեշտ է այն ձախից լրացնել զերոներով: Օրինակ` \(101001\) կոդը պարունակում է ընդամենը \(6\) պայմանանշան, հետևաբար լրիվ կոդը կլինի \(00101001\): Նկատենք, որ ստացվածը կոդային աղյուսակում համապատասխանում է \(«)»\) պայմանանշանին:
Ընդհանրապես` երկուական համակարգով կոդավորված տեքստային ինֆորմացիան հասկանալու համար անհրաժեշտ է երկուական թիվն աջից դեպի ձախ բաժանել ութնյակների (կիսատ ձախ եզրային ութնյակը լրացնել զրոներով) և յուրաքանչյուր նման ութնյակ փոխարինել համապատասխան պայմանանշանով:
Օրինակ` վերծանենք \(11101010111000011101110110110011\) երկուական կոդը:
Դրա համար, նախ, այն աջից բաժանենք ութնյակների` \(11101010\ 11100001\ 11011101\ 10110011\), ապա կոդային աղյուսակի օգնությամբ կցագրենք յուրաքանչյուր ութնյակին համապատասխանող պայմանանշանը: Կստանանք Սոնա գրառումը:
Համեմատության համար դիտարկենք հետևյալ օրինակը: Հաշվարկներում տասական \(25\)թվի երկուական կոդը կներկայացվի մեկ բայթի մեջ` \(00011001\) գրառմամբ, իսկ տեքստի մեջ` երկու բայթում, \(00110010\ 00110101\) գրառմամբ:
Ինչպես գիտեք, կետային գրաֆիկական խմբագրիչի միջավայրում ստեղծված պատկերները բաղկացած են առանձին կետերից` փիքսելներից: Համակարգչում կետային պատկերը կոդավորելիս, դրա գրաված ծավալը որոշվում է պատկերը պարունակող կետերի թվի և մեկ կետի ինֆորմացիոն ծավալի արտադրյալով: Վերջինս կախված է կետի ընդունած գույների հնարավոր քանակից:
Սև-սպիտակ կետային պատկերի վրա ցանկացած կետի կոդը մեկ բիթ հիշողություն է զբաղեցնում, քանի որ կետը կարող է լինել սև կամ սպիտակ, և, հետևաբար` այստեղ յուրաքանչյուր կետ կարելի է կոդավորել 0 կամ 1 թվանշանների միջոցով: Նկարի յուրաքանչյուր դատարկ վանդակ կոդավորելով 0 թվով, իսկ ներկած վանդակը` 1 թվով, կարելի է ստանալ նկարի կոդը:
Նկարում բերված օրինակում պատկերի հատվածը բաղկացած է \(14x17=238\) կետից և քանի որ յուրաքանչյուր կետի կոդ զբաղեցնում է մեկ բիթ հիշողություն, ապա հատվածի կոդավորման համար կպահանջվի \(238\) բիթ ծավալով հիշողություն:
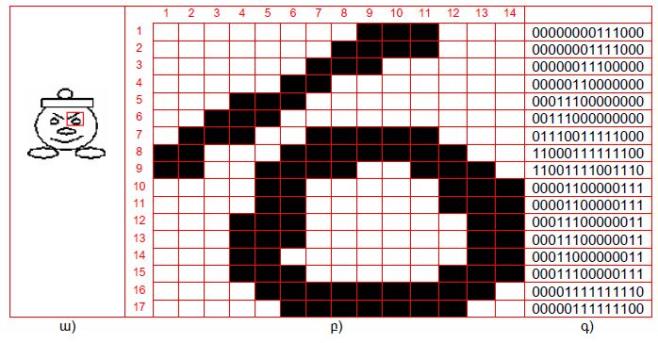
Պատկերի
ա) բնական տեսքը, բ) հատվածի խոշորացված տեսքը, գ) հատվածի կոդը
ա) բնական տեսքը, բ) հատվածի խոշորացված տեսքը, գ) հատվածի կոդը
Գունավոր պատկերի յուրաքանչյուր կետ, որը կարող է ներկված լինել \(16\)գույներով ներկապնակի գույներից որևէ մեկով կոդավորվում է \(4\) բիթի օգնությամբ:
Նման կոդավորման դեպքում նկարում բերված պատկերի հատվածը կզբաղեցնի \(14x17x4=952\) բիթ ծավալով հիշողություն:
Ուշադրություն
Ի տարբերություն կետային գրաֆիկայի, վեկտորային պատկերների կոդավորումն իրականացվում է տարբեր եղանակներով: Մասնավորապես` պատկերի բաղադրիչ գրաֆիկական միավորները նկարագրող բանաձևերը կարող են կոդավորվել որպես սովորական տառա-թվային ինֆորմացիա, որը հետագայում կվերամշակվի հատուկ ծրագրերի օգնությամբ: