Տեքստային խնդիրների լուծումը համակարգերի օգնությամբ

Երկու փոփոխականով երկու հավասարումների համակարգերի միջոցով հաճախ լուծվում են տեքստային խնդիրներ:

Տեքստային խնդրի լուծման ընթացքը բաժանվում է երեք փուլի:

Առաջին փուլ՝ համակարգի կազմում:

Երկրորդ փուլ՝ համակարգի լուծում:

Երրորդ փուլ՝ խնդրի պատասխան:

Օրինակ

Խնդիր: Ուղղանկյուն եռանկյան էջերի տարբերությունը \(23\) սմ է, իսկ ներքնաձիգը՝ \(37\) սմ:

Պետք է գտնել եռանկյան մակերեսը:

Լուծում:

Առաջին փուլ՝ համակարգի կազմում:

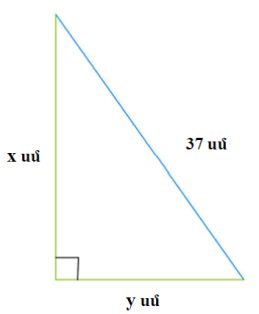
Էջերից մեկի երկարությունը նշանակենք \(x\) սմ, իսկ մյուսը՝ \(y\) սմ:

Ուրեմն էջերի տարբերությունը կլինի

x - y = 23

Կիրառելով Պյութագորասի թեորեմը, ստանում ենք երկրորդ հավասարումը՝

\begin{array}{l} x^{2} + y^{2} = 37^{2} \\ x^{2} + y^{2} = 1369 \end{array}

Կազմում ենք երկու անհայտով համակարգ՝

\{\begin{cases} x - y = 23 \\ x^{2} + y^{2} = 1369 \end{cases}

Երկրորդ փուլ՝ համակարգի լուծում:

Առաջին հավասարումից \(x\)-ը արտահայտենք \(y\)-ով՝

\{\begin{cases} x = 23 + y \\ x^{2} + y^{2} = 1369 \end{cases}

\(x\)-ի ստացված արտահայտությունը տեղադրենք երկրորդ հավասարման մեջ՝

\begin{array}{l} x^{2} + y^{2} = 1369 \\ {(23 + y)}^{2} + y^{2} = 1369 \\ 23^{2} + 46 y + y^{2} + y^{2} = 1369 \\ 2 y^{2} + 46 y + 529 - 1369 = 0 \\ 2 y^{2} + 46 y - 840 = 0 |: 2 \\ y^{2} - 23 y - 420 = 0 \\ y_{1} = \underline{12} \end{array}

y_{2} = - 35

(չի բավարարում խնդրի պայմանին)

\(x\)-ը գտնենք առաջին հավասարումից՝

x = 23 + 12 = \underline{35}

Երրորդ փուլ՝ խնդրի պատասխան

Գտնենք եռանկյան մակերեսը:

S = \frac{1}{2} xy = \frac{1}{2} \cdot 12 \cdot 35 = \frac{{}^{6}12 \cdot 35}{2_{1}} = 210 {սմ}^{2}

Պատասխան՝

S = 210 {սմ}^{2}

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013

Սխա՞լ ես գտել

1. Տեքստային խնդիրների լուծումը համակարգերի օգնությամբ