
















ֆունկցիան և նրա գրաֆիկը
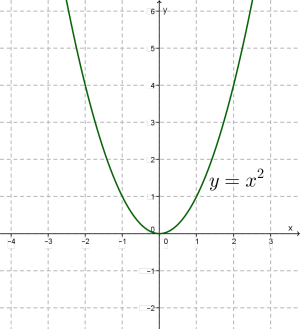
Քննարկենք, թե ի՞նչ է կատարվում \(k\)-ի այլ արժեքների դեպքում:
Դիտարկենք հետևյալ երկու ֆունկցիաները՝ և
Կազմենք ֆունկցիայի արժեքների աղյուսակը՝
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(1.5\) | \(-1.5\) |
| \(y\) | \(0\) | \(2\) | \(2\) | \(8\) | \(8\) | \(4.5\) | \(4.5\) |
Կոորդինատային հարթության վրա կառուցենք ստացված \((0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5)\) կետերը և միացնենք դրանք կորով:
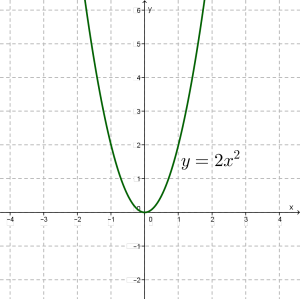
Կազմենք ֆունկցիայի արժեքների աղյուսակը՝
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) |
| \(y\) | \(0\) | \(0.5\) | \(0.5\) | \(2\) | \(2\) | \(4.5\) | \(4.5\) |
Կոորդինատային հարթության վրա կառուցենք ստացված \((0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), (3; 4,5), (-3; 4,5)\) կետերը և միացնենք դրանք կորով:
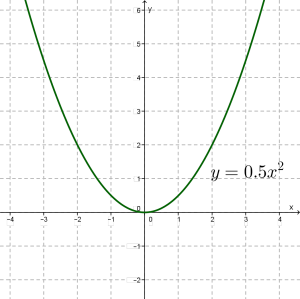
Համեմատենք ստացված գրաֆիկները: Դրանք նման են իրար, երկուսն էլ կոչվում են պարաբոլ:
\((0; 0)\) կետը կոչվում է պարաբոլի գագաթ, իսկ \(y\)-երի առանցքը՝ պարաբոլի համաչափության առանցք:
Ուշադրություն
\(k\)-ի արժեքից կախված է պարաբոլի ճյուղերի թեքությունը:
Նման տեսք ունեն նաև մյուս տեսքի ֆունկցիաների գրաֆիկները, որտեղ \(k > 0\)
Դրանց բոլորի գրաֆիկը պարաբոլ է, որի գագաթը կոորդինատների սկզբնակետն է, ճյուղերը ուղղված են դեպի վերև: Որքան մեծ է \(k\)-ն, այնքան ավելի կտրուկ են բարձրանում պարաբոլի ճյուղերը, \(y\)-երի առանցքը պարաբոլի համաչափության առանցքն է:
Հիմա պարզենք, թե ի՞նչ է կատարվում ֆունկցիայի գրաֆիկի հետ, եթե \(k\)-ն բացասական է:
Կառուցենք, օրինակ՝ ֆունկցիայի գրաֆիկը (\(k = - 1\))
Կազմենք արժեքների աղյուսակը՝
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) |
| \(y\) | \(0\) | \(-1\) | \(-1\) | \(-4\) | \(-4\) | \(-9\) | \(-9\) |
Նշենք \((0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; - 9)\) կետերը և միացնենք կորով:
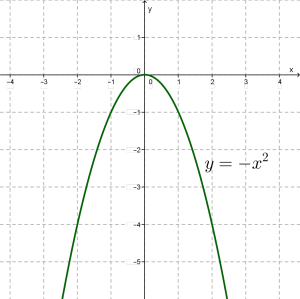
Այս պարաբոլի գագաթը ևս \((0; 0)\) կետն է և \(y\)-երի առանցքը նրա համաչափության առանցքն է: Սակայն, ի տարբերություն \(k > 0\) դեպքի, այս պարաբոլի ճյուղերը ուղղված են դեպի ներքև: Նման տեսք ունեն նաև բացասական \(k\)-ով մյուս պարաբոլները:
Ուշադրություն
Այսպիսով, ֆունկցիայի գրաֆիկը պարաբոլ է, որի գագաթը կոորդինատների սկզբնակետն է և \(y\)-երի առանցքը նրա համաչափության առանցքն է: Եթե \(k>0\), ապա պարաբոլի ճյուղերը ուղղված են դեպի վերև, եթե \(k<0\), ապա ճյուղերը ուղղված են դեպի ներքև:
Եթե նույն կոորդինատային համակարգում կառուցենք և ֆունկցիաների գրաֆիկները, ապա կնկատենք, որ այդ պարաբոլները համաչափ են իրար \(x\)-երի առանցքի նկատմամբ: Դա լավ երևում է ներքևի նկարում:
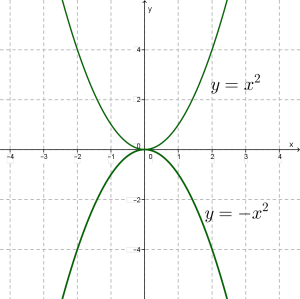
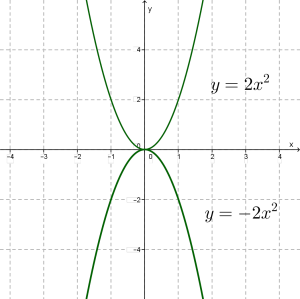
Նույն կերպ \(x\)-երի առանցքի նկատմամբ համաչափ են և պարաբոլները:
Ուշադրություն
Ընդհանուր առմամբ, \(у = - f(x)\) և \(у = f(x)\) ֆունկցիաների գրաֆիկները համաչափ են աբսցիսների առանցքի նկատմամբ:
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013: