y=ax² ֆունկցիան — դաս։ Հանրահաշիվ, 9-րդ դասարան.

y=ax² ֆունկցիան

Ամփոփենք արդեն ասվածը

y = {ax}^{2}

ֆունկցիայի հատկությունների և գրաֆիկի վերաբերյալ:

y = a x^{2} (a \neq 0)

ֆունկցիայի գրաֆիկը պարաբոլ է, որի գագաթը կոորդինատների սկզբնակետն է:

	$a > 0$	$a < 0$
Գրաֆիկի տեսքը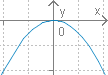
Գրաֆիկի դիրքը	Ճյուղերն ուղղված են դեպի վերև	Ճյուղերն ուղղված են դեպի ներքև
Աճման և նվազման միջակայքերը	Նվազում է, եթե $x \in (- \infty; 0]$ , աճում է, եթե $x \in [0; + \infty)$	Աճում է, եթե $x \in (- \infty; 0]$ , նվազում է, եթե $x \in [0; + \infty)$
Մեծագույն արժեքը	չկա	$y = 0$
Փոքրագույն արժեքը	$y = 0$	չկա
Նշանապահպանման միջակայքերը	($y > 0$), եթե $x \in (- \infty; 0) \cup (0; + \infty)$ (գրաֆիկը $Ox$ առանցքից վերև)	չկա
	չկա	($y < 0$), եթե $x \in (- \infty; 0) \cup (0; + \infty)$ (գրաֆիկը $Ox$ առանցքից ներքև)

Գրաֆիկը համաչափ է $Oy$ առանցքի նկատմամբ:

Որքան մեծ է գործակցի մոդուլը՝ $| a |$-ն, այդքան ճյուղերը մոտ են $Oy$ առանցքին:

y = 5 x^{2}

y = 0, 2 x^{2}

y = {ax}^{2}

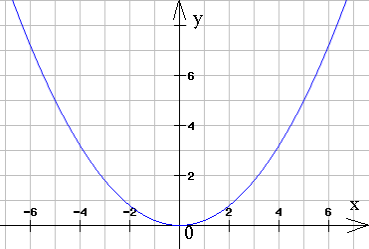գրաֆիկը կառուցում են աղյուսակի միջոցով:

Օրինակ

Աղյուսակը լրացնենք

y = 3 x^{2}

ֆունկցիայի համար: Հաշվենք ֆունկցիայի արժեքները, եթե արգումենտը հավասար է $1;-1;2;-2$

$x$	$-2$	$-1$	$1$	$2$
$y$	$3 \cdot {(- 2)}^{2} = 3 \cdot 4 = \underline{12}$	$3 \cdot {(- 1)}^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 1^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 2^{2} = 3 \cdot 4 = \underline{12}$

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:

Սխա՞լ ես գտել

\(x\)	\(-2\)	\(-1\)	\(1\)	\(2\)
\(y\)	$3 \cdot {(- 2)}^{2} = 3 \cdot 4 = \underline{12}$	$3 \cdot {(- 1)}^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 1^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 2^{2} = 3 \cdot 4 = \underline{12}$

3. y=ax² ֆունկցիան