1. у = f(x) + m ֆունկցիայի գրաֆիկի կառուցումը у = f(x) ֆունկցիայի գրաֆիկի միջոցով

Ինչպե՞ս կառուցել \(у = f(x) + m\)  ֆունկցիայի գրաֆիկը, եթե տրված է  \(у = f(x)\)-ի  գրաֆիկը
Նույն կոորդինատային համակարգում կառուցենք y=x2 և y=x2+4 ֆունկցիաների գրաֆիկները: Կազմենք y=x2+4 ֆունկցիայի արժեքների աղյուսակը՝
 
\(x\)\(0\)\(1\)\(-1\)\(2\)\(-2\)
\(y\)\(4\)\(5\)\(5\)\(8\)\(8\)
 
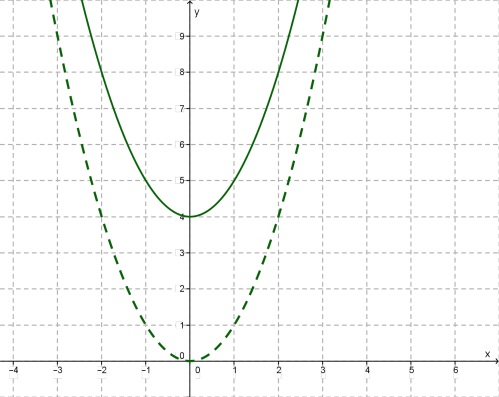
Կոորդինատային հարթության վրա նշենք գտնված \((0; 4), (1; 5), (-1; 5), (2; 8), (-2; 8)\) կետերը և միացնենք դրանք կորով: Կստանանք պարաբոլ՝
 
001.png
 
Ուշադրություն
Սա նույն y=x2 պարաբոլն է, որը \(y\)-երի առանցքով տեղաշարժված է \(4\) միավորով դեպի վերև: Պարաբոլի գագաթը հիմա գտնվում է \((0; 4)\) կետում, ոչ թե՝ \((0; 0)\) կետում, ինչպես y=x2 պարաբոլի դեպքում: Համաչափության առանցքը մնում է \(x = 0\) առանցքը, ինչպես և y=x2 դեպքում:
Իսկ եթե նույն կոորդինատային համակարգում կառուցենք y=x2 և y=x2−2 ֆունկցիաների գրաֆիկները, ապա կնկատենք, որ երկրորդ գրաֆիկը ստացվում է առաջինի տեղաշարժով \(y\)-երի առանցքի ուղղությամբ՝ \(2\) միավորով դեպի ներքև:
 
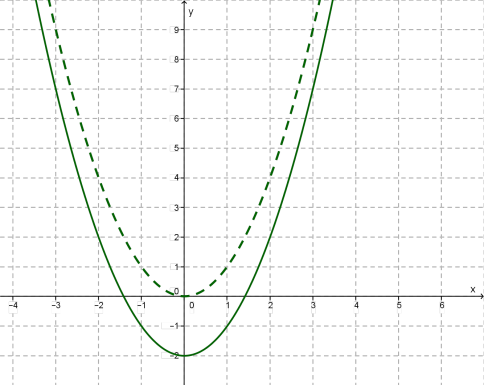
002.png
 
Նույն կերպ գրաֆիկները կառուցվում են նաև մյուս դեպքերում: Օրինակ՝  y=2x2−3 ֆունկցիայի գրաֆիկը ստացվում է y=2x2 պարաբոլի տեղաշարժով \(y\)-երի առանցքի ուղղությամբ՝ \(3\) միավորով դեպի ներքև:
 
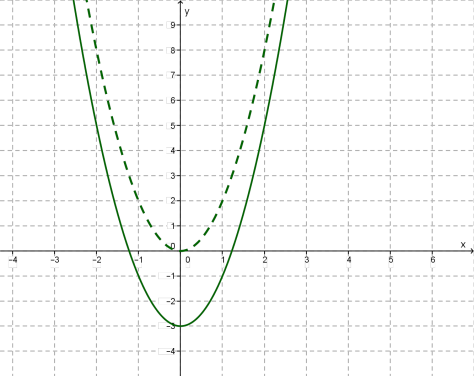
003.png
 
Ընդհանուր դեպքում ճիշտ է հետևյալ պնդումը՝ 
1) \(y = f(x) + m\), որտեղ \(m\)-ը տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել  \(y= f(x)\) ֆունկցիայի գրաֆիկը \(y\)-երի առանցքի ուղղությամբ՝ \(m\) միավորով դեպի վերև:  
 
2) \(y = f(x) - m\), որտեղ \(m\)-ը տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել  \(y= f(x)\) ֆունկցիայի գրաֆիկը \(y\)-երի առանցքի ուղղությամբ՝ \(m\) միավորով դեպի ներքև:
Ուշադրություն
Տեղաշարժի նշանը որոշվում է \(m\) թվի նշանով: Եթե \(m > 0\), ապա պետք է տեղաշարժել դեպի վերև, իսկ եթե \(m < 0\), ապա՝ դեպի ներքև:  
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013
Վերադառնալ թեմային
Հաջորդ առաջադրանքը
Copyright © 2024 ԻմԴպրոց ՍՊԸ