2. Ֆունկցիայի նշանապահպանման միջակայքերը և զրոները

1. Գտնենք այս ֆունկցիայի որոշման տիրույթը:

 

Ֆունկցիան որոշված է բոլոր այն թվերի համար, որոնց դեպքում արմատատակ արտահայտությունը բացասական չէ, և հայտարարը զրո չի դառնում՝

 

 $\left\{\begin{array}{l}x\ge -1\\ x\ne 4\end{array}\right.$

 

Այսպիսով, ֆունկցիայի որոշման տիրույթը $[-1;4)\cup (4;+\mathrm{\infty })$ բազմությունն է:

 

 

2. Գտնենք այս ֆունկցիայի զրոները:

 

Լուծենք $f\left(x\right)=0$ հավասարումը: Որպեսզի կոտորակը հավասար լինի զրոյի, պետք է զրո լինի

 

նրա համարիչը՝ $\begin{array}{l}\sqrt{x+1}=0\\ x+1=0\\ x=-1\end{array}$

 

Այսպիսով, ֆունկցիայի միակ զրոն $x_0=-1$-ն է:

 

3. Գտնենք այս ֆունկցիայի նշանապահպանման միջակայքերը:

 

Քանի որ քառակուսի արմատը՝ կոտորակի համարիչը, երբեք բացասական չի դառնում, ապա կոտորակի նշանը կախված է նրա հայտարարի նշանից: Եթե հայտարարը դրական է, ապա դրական է նաև ամբողջ կոտորակը, իսկ եթե հայտարարը բացասական է, ապա բացասական է նաև կոտորակը: Ստանում ենք ֆունկցիայի նշանապահպանման հետևյալ պատկերը՝

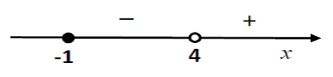
Այսպիսով, ֆունկցիան բացասական է $(-1;4)$ միջակայքում և դրական է $(4;+\mathrm{\infty })$ միջակայքում: