
















Ռացիոնալ անհավասարումների լուծման միջակայքերի եղանակը
Մեկ \(x\) փոփոխականով ռացիոնալ անհավասարում անվանում են տեսքի անհավասարումը, որտեղ \(f(x)\)-ը և \(g(x)\)-ը \(x\) փոփոխականի նկատմամբ բազմանդամներ են:
Ռացիոնալ անհավասարումները լուծելիս օգտագործում են գծային և քառակուսային անհավասարումների լուծման եղանակները: Մասնավորապես, հաճախ օգտագործվում է միջակայքերի եղանակը:
Օրինակ
Լուծենք անհավասարումը:
Լուծում
1. Գտնենք քառակուսային եռանդամի արմատները
և բանաձևի միջոցով այն վերլուծենք արտադրիչների՝
2. Անհավասարման երկու մասերը բաժանենք դրական արտահայտության վրա (անհավասարման «\(>\)» նշանը չի փոխվում):
3. Թվային առանցքի վրա գտնենք քառակուսային եռանդամի արմատները և պարզենք եռանդամի արժեքները առաջացած միջակայքերից յուրաքանչյուրում: Դրա համար բավական է յուրաքանչյուր միջակայքից վերցնել մեկական թիվ և այն տեղադրել եռանդամի մեջ \(x\)-ի փոխարեն:
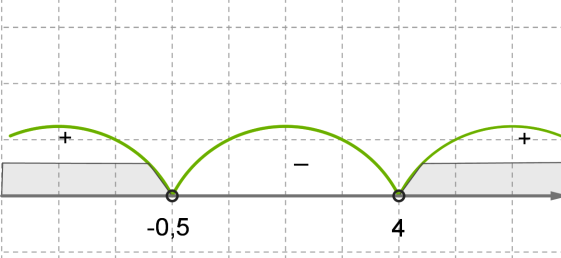
միջակայքից վերցնենք \(x=-2\) կետը, ապա
միջակայքից վերցնենք \(x=0\) կետը, ապա
միջակայքից վերցնենք \(x=5\) կետը, ապա
Քառակուսային եռանդամը դրական է և միջակայքերում:
Պատասխան՝ և
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013: