Անհավասարումների լուծման միջակայքերի եղանակը

Հաճախ հարմար է քառակուսային անհավասարումները լուծել միջակայքերի եղանակով:

Դիտարկենք միջակայքերի եղանակի քայլերը՝

• գտնել

a x^{2} + bx + c

քառակուսային եռանդամի արմատները և այն վերլուծել արտադրիչների

• արմատները տեղադրել կոորդինատային առանցքի վրա և պարզել եռանդամի նշանները առաջացած միջակայքերից յուրաքանչյուրում

• ընտրել անհավասարման նշանին համապատասխան միջակայքը և այն գրել որպես պատասխան

Լուծենք

2 x^{2} - 7 x - 4 \leq 0

անհավասարումը:

Օրինակ

Լուծում: Գտնենք

2 x^{2} - 7 x - 4

եռանդամի արմատները և այն

a x^{2} + bx + c = a (x - x_{1}) (x + x_{1})

բանաձևով վերլուծենք արտադրիչների:

\begin{array}{l} 2 x^{2} - 7 x - 4 = 0 \\ D = b^{2} - 4 ac = {(- 7)}^{2} - 4 \cdot 2 \cdot (- 4) = 49 + 32 = 81 \\ x_{1} = \frac{- b - \sqrt{D}}{2 a} = \frac{- (- 7) - \sqrt{81}}{2 \cdot 2} = \frac{7 - 9}{4} = \frac{- 2}{4} = - \frac{1}{2} = - 0,5 \\ x_{2} = \frac{- b + \sqrt{D}}{2 a} = \frac{- (- 7) + \sqrt{81}}{2 \cdot 2} = \frac{7 + 9}{4} = \frac{16}{4} = 4 \\ 2 x^{2} - 7 x - 4 = 2 (x + 0,5) (x - 4) \\ 2 (x + 0,5) (x - 4) = 0 |: 2 \\ (x + 0,5) (x - 4) = 0 \\ x_{1} = - 0,5 x_{2} = 4 \end{array}

Կոորդինատային առանցքի վրա տեղադրենք գտած արմատները և պարզենք եռանդամի նշանները առաջացած միջակայքերում:

Դրա համար բավական է յուրաքանչյուր միջակայքից վերցնել մեկական թիվ և այն \(x\)-ի փոխարեն տեղադրել եռանդամի մեջ:

(- \infty; - 0,5]

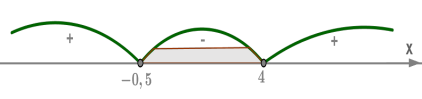
միջակայքից վերցնենք \(x=-2\) թիվը, ապա՝

2 {\cdot (- 2)}^{2} - 7 \cdot (- 2) - 4 = 2 \cdot 4 + 14 - 4 = 18 > 0

[- 0,5; 4]

միջակայքից վերցնենք \(x=0\), թիվը, ապա՝

2 {\cdot 0}^{2} - 7 \cdot 0 - 4 = 0 - 0 - 4 = - 4 < 0

[4; + \infty)

միջակայքից վերցնենք \(x=5\), թիվը, ապա՝

2 {\cdot 5}^{2} - 7 \cdot 5 - 4 = 2 \cdot 25 - 35 - 4 = 50 - 39 = 11 > 0

Քառակուսային եռանդամի արժեքները ընդունում են բացասական և զրո արժեքներ

[- 0,5; 4]

հատվածի վրա:

Պատասխան՝

- 0,5 \leq x \leq 4

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:

Սխա՞լ ես գտել

1. Անհավասարումների լուծման միջակայքերի եղանակը