
















Բաց և փակ միջակայքեր թվային առանցքի վրա
Սրանք, այսպես կոչված, անսահմանափակ բազմություններ (մի կողմից կամ երկու կողմից) են: Դիտարկենք սահմանափակ բազմություններ թվային առանցքի վրա:
Եթե \(x\) թիվը միաժամանակ բավարարում է \(x>-4\) և \(x<5\) անհավասարություններին, ապա այն բավարարում է \(-4<x<5\) երկկողմանի անհավասարությանը:
\(-4<x<5\) երկկողմանի անհավասարությանը բավարարող բոլոր թվերի բազմությունը անվանում են թվային միջակայք և նշանակում են այսպես՝ \((-4;5)\):
Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «\(-4\), \(5\) ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):
Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «\(-4\), \(5\) ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):
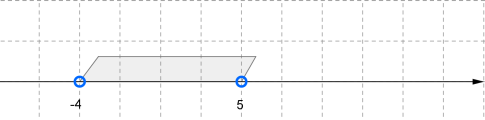
Դիտարկենք ուրիշ միջակայքեր:
կամ : Կարդում ենք՝ «\(-4\), \(5\) հատված», կամ «փակ միջակայք»: Նկատենք, որ հատվածի ծայրակետերը ընդգրկված են (սևացված են):
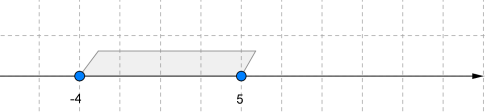
կամ : Կարդում ենք՝ «\(-4\), \(5\) կիսաինտերվալ», կամ «կիսաբաց միջակայք»: Նկատենք, որ կիսաինտերվալի ծայրակետերից մեկը՝ \(-4\) -ը ընդգրկված է (սևացված է), իսկ մյուսը՝ \(5\) -ը ընդգրկված չէ (սևացված չէ):
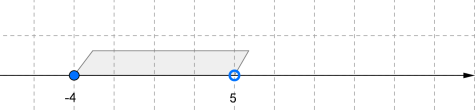
կամ : Սա ևս կիսաինտերվալ է՝ բաց ձախ ծայրակետով:

Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012: