y=1/x ֆունկցիայի գրաֆիկը — դաս։ Հանրահաշիվ, 8-րդ դասարան.

y = \frac{k}{x}

ֆունկցիան

Ծանոթանանք նոր ֆունկցիայի հետ՝

y = \frac{k}{x}

$k$ գործակիցը կարող է ընդունել ցանկացած արժեքներ, բացի $k = 0$ դեպքից: Սկզբում դիտարկենք $k = 1$ դեպքը: Այսպիսով, խոսքը

y = \frac{1}{x}

ֆունկցիայի մասին է:

y = \frac{1}{x}

ֆունկցիայի գրաֆիկը կառուցելու համար $x$ անկախ փոփոխականին տանք մի քանի որոշակի արժեքներ և

y = \frac{1}{x}

բանաձևով հաշվենք $y$ կախյալ փոփոխականի համապատասխան արժեքները: Հարմար է սկզբում արգումենտին տալ դրական արժեքներ, հետո կդիտարկենք նաև բացասականները:

Առաջին քայլ: Եթե $x = 1$, ապա $y = 1$ (հիշիր, որ մենք օգտվում ենք

y = \frac{1}{x}

բանաձևից):

Եթե $x = 2$, ապա

y = \frac{1}{2}

եթե $x = 4$, ապա

y = \frac{1}{4}

եթե $x = 8$, ապա

y = \frac{1}{8}

եթե

x = \frac{1}{2}

, ապա $y = 2$

եթե

x = \frac{1}{4}

, ապա $y = 4$

եթե

x = \frac{1}{8}

, ապա $y = 8$

Այսպիսով, լրացրինք հետևյալ աղյուսակը:

$x$	$1$	$2$	$4$	$8$	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$
$y$	$1$	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$	$2$	$4$	$8$

$xOy$ հարթության վրա կառուցենք գտնված կետերը:

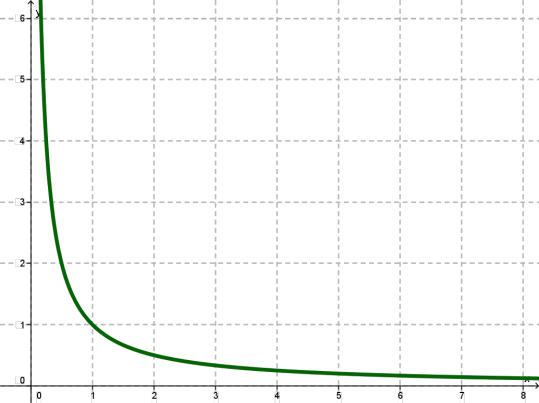
Երկրորդ քայլ:

Եթե $x = -1$, ապա $y = -1$,

եթե $x = -2$, ապա

y = - \frac{1}{2}

եթե $x= -4$, ապա

y = - \frac{1}{4}

եթե $x = -8$, ապա

y = - \frac{1}{8}

եթե

x = - \frac{1}{2}

, ապա $y = -2$

եթե

x = - \frac{1}{4}

, ապա $y = -4$

եթե

x = - \frac{1}{8}

, ապա $y = -8$

Լրացրինք հետևյալ աղյուսակը:

$x$	$-1$	$-2$	$-4$	$-8$	$-$ $\frac{1}{2}$	$-$ $\frac{1}{4}$	$-$ $\frac{1}{8}$
$y$	$-1$	$-$ $\frac{1}{2}$	$-$ $\frac{1}{4}$	$-$ $\frac{1}{8}$	$-2$	$-4$	$-8$

$xOy$ հարթության վրա կառուցենք գտնված կետերը:

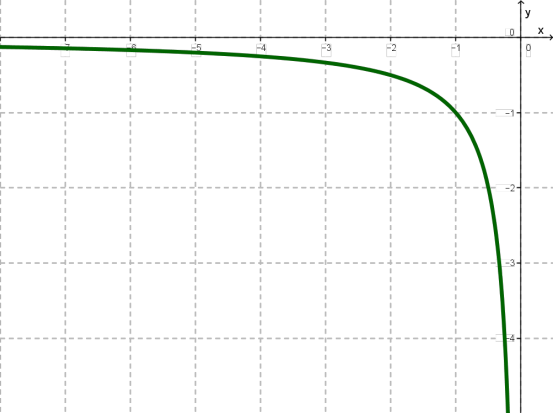
Երրորդ քայլ: Հիմա միացնենք առաջին երկու քայլերը: Նույն գծագրի վրա կառուցենք առաջին և երկրորդ գրաֆիկները:

Սա հենց

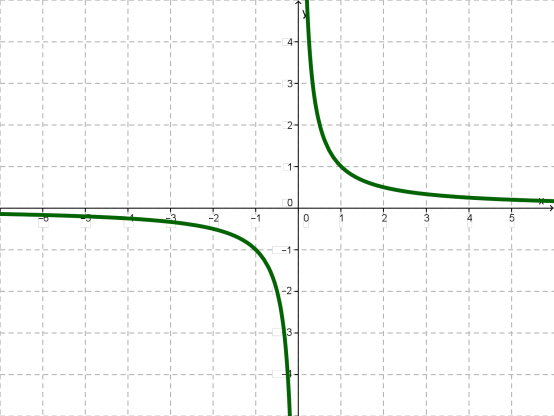
y = \frac{1}{x}

ֆունկցիայի գրաֆիկն է: Այն կոչվում է հիպերբոլ:

Թվարկենք հիպերբոլի մի քանի երկրաչափական հատկություններ, որոնք բխում են կառուցված գրաֆիկից:

Նախ և առաջ, նկատում ենք, որ առաջին և երրորդ քառորդներով և կոորդինատների $O$ սկզբնակետով անցնող ցանկացած ուղիղ հիպերբոլը հատում է երկու կետերում, որոնք ընկած են $O$ կետից հավասար հեռավորությունների վրա, բայց տարբեր կողմերում: Այդպիսին են, օրինակ՝ $(1; 1)$ և $(- 1; - 1)$,

(2; \frac{1}{2})

(- 2; - \frac{1}{2})

և այլ կետեր:

1) Հետևաբար, $O$ կետը հիպերբոլի համաչափության կենտրոնն է: Կամ ասում են, որ հիպերբոլը կենտրոնական համաչափ է կոորդինատների սկզբնակետի նկատմամբ:

2) Հիպերբոլը բաղկացած է կոորդինատների սկզբնակետի նկատմամբ համաչափ երկու մասերից, որոնք կոչվում են հիպերբոլի ճյուղեր:

3) Նկատում ենք, որ հիպերբոլի ճյուղերը մի ուղղությամբ անընդհատ մոտենում են աբսցիսների առանցքին, իսկ մյուս ուղղությամբ՝ օրդինատների առանցքին: Այդպիսի դեպքերում համապատասխան ուղիղները անվանում են ասիմպտոտներ:

Այսպիսով

y = \frac{1}{x}

ֆունկցիայի գրաֆիկը՝ հիպերբոլն ունի երկու ասիմպտոտ՝ $x$ -երի առանցքը և $y$ -երի առանցքը:

Եթե ուշադիր նայենք կառուցված գրաֆիկին, ապա կնկատենք հիպերբոլի ևս մեկ հատկություն:

4) Հիպերբոլն ունի համաչափության առանցք, որը տրվում է $y = x$ հավասարմամբ:

Ուշադրություն

Այսպիսով, հիպերբոլն ունի և՛ համաչափության կենտրոն, և՛ համաչափության առանցք:

Իրոք, դիտարկենք $y = x$ ուղիղը:

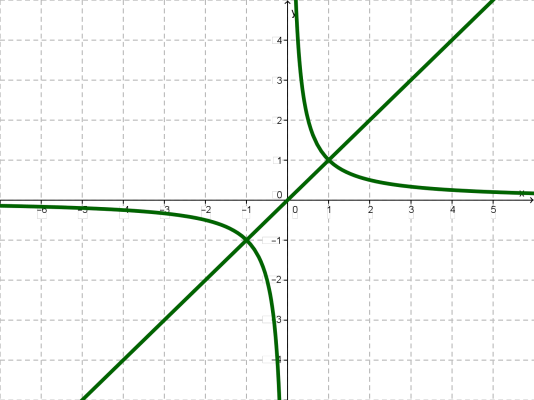
Հիմա նկատում ենք, որ

(2; \frac{1}{2}) և (\frac{1}{2}; 2)

կետերը գտնվում են նույն հեռավորության վրա տարված ուղղից, բայց՝ տարբեր կողմերում: Նրանք համաչափ են տարված ուղղի նկատմամբ: Նույնը կարելի է ասել նաև

(4; \frac{1}{4}) և (\frac{1}{4}; 4), (8; \frac{1}{8}) և (\frac{1}{8}; 8)

և շատ ուրիշ կետերի մասին: Դա նշանակում է, որ $y =x$ ուղիղը համաչափության առանցք է

y = \frac{1}{x}

հիպերբոլի համար:

Ուշադրություն

Հիպերբոլն ունի համաչափության ևս մեկ առանցք, դա երկրորդ և չորրորդ քառորդներով և կոորդինատների սկզբնակետով անցնող $y = -x$ ուղիղն է:

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

\(x\)	\(1\)	\(2\)	\(4\)	\(8\)	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$
\(y\)	\(1\)	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$	\(2\)	\(4\)	\(8\)

\(x\)	\(-1\)	\(-2\)	\(-4\)	\(-8\)	\(-\) $\frac{1}{2}$	\(-\) $\frac{1}{4}$	\(-\) $\frac{1}{8}$
\(y\)	\(-1\)	\(-\) $\frac{1}{2}$	\(-\) $\frac{1}{4}$	\(-\) $\frac{1}{8}$	\(-2\)	\(-4\)	\(-8\)

1. y=1/x ֆունկցիայի գրաֆիկը

Տեսություն